题目内容
12.如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN过点C,且AD⊥MN于点D,BE⊥MN于点E,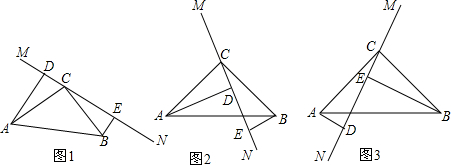
(1)这时,DE、AD、BE的数量关系是:DE=AD+BE.并写出图中的一对全等三角形:答△ADC≌△CEB;
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,DE、AD、BE又怎么样的数量关系?答:DE=BE-AD.
分析 (1)由于△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,由此即可证明△ADC≌△CEB,然后利用全等三角形的性质即可解决问题;
(2)由于△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,由此仍然可以证明△ADC≌△CEB,然后利用全等三角形的性质也可以解决问题;
(3)当直线MN绕点C旋转到图(3)的位置时,仍然△ADC≌△CEB,然后利用全等三角形的性质可以得到DE=BE-AD.
解答 解:(1)∵△ABC中,∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°
∴∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠ECB}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴CD=BE,CE=AD,
∴DE=CD+CE=AD+BE;
(2)∵△ABC中,∠ACB=90°,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠ACD+∠BCE=∠BCE+∠CBE=90°,
而AC=BC,
∴△ADC≌△CEB,
∴CD=BE,CE=AD,
∴DE=CE-CD=AD-BE;
(3)如图3,
∵△ABC中,∠ACB=90°,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠ACD+∠BCE=∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
∵AC=BC,
∴△ADC≌△CEB,
∴CD=BE,CE=AD,
∴DE=CD-CE=BE-AD;
DE、AD、BE之间的关系为DE=BE-AD.
点评 本题考查了三角形全等的判定与性质,关键是利用全等三角形对应线段相等,将有关线段进行转化.

 学业测评一课一测系列答案
学业测评一课一测系列答案| 原料 | 甲 | 乙 |
| 维生素 | 600单位 | 100单位 |
| 原料价格 | 8元 | 4元 |
| A. | $\left\{\begin{array}{l}{600x+100x≥4200}\\{8(10-x)+4(10-x)≤72}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{600x+100(10-x)≥4200}\\{8x+4(10-x)≤72}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{600x+100x>4200}\\{8(10-x)+4(10-x)<72}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{600x+100x<4200}\\{8(10-x)+4(10-x)>72}\end{array}\right.$ |
| A. | x+y | B. | $\frac{x+y}{2}$ | C. | $\frac{xy}{x+y}$ | D. | $\frac{x+y}{xy}$ |
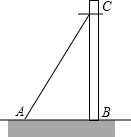 如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.
如图,要从电线杆离地面的C处向地面A处拉一条长10m的电缆,测得∠CAB=60°,则电线杆的高度BC是5$\sqrt{3}$m.
 如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:
如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:
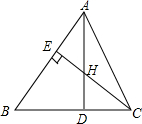 如图,AD是△ABC的角平分线,CE是△ABC的高线,AD与CE交于点H.已知∠BAC=60°,∠B=50°,求∠ADC和∠CHD的度数.
如图,AD是△ABC的角平分线,CE是△ABC的高线,AD与CE交于点H.已知∠BAC=60°,∠B=50°,求∠ADC和∠CHD的度数.