题目内容
8．若x，y为实数，且满足|x-3|+$\sqrt{y+3}$=0，则（$\frac{x}{y}$）2015的立方根是（ ）| A． | 1 | B． | -1 | C． | 2 | D． | 3 |
分析 根据非负数的性质列式求出x、y的值，然后代入代数式进行计算即可得解．
解答 解：由题意得，x-3=0，y+3=0，
解得x=3，y=-3，
所以（$\frac{x}{y}$）2015=（$\frac{3}{-3}$）2015=-1．
故选：B．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
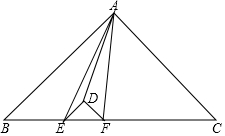如图，等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上，连接AE、AD、AF，于是整个图形被分成五块小三角形．其中三块的面积为S△DEF=1、S△ADE=2、S△ADF=3，那么△ABC的面积是36．
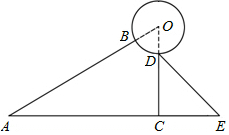如图是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O，支架CD与水平面AE垂直，AB=150厘米，∠BAC=30°，另一根辅助支架DE=40$\sqrt{3}$厘米，∠CED=60°．
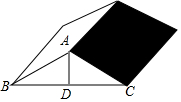如图所示是某工厂长方屋顶的人字架（等腰三角形），它的跨度BC=12米，中柱AD为2.5米，中柱AD⊥BC，且垂足D为BC的中点，又知厂房长20米，为防雨，需在房顶铺满油毡．（每卷油毡宽1米，长10米），如果你是该厂采购，需购买多少卷油毡？
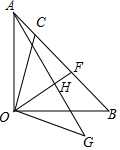如图，△AOB为等腰直角三角形，∠AOB=90°，C是线段AB上一点，连接OC，作OG⊥OC，且OC=OG，连接AG，取CF=FB，连OF交AG于H，求证：OH⊥AG．
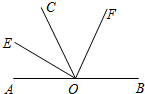如图，O为直线AB上一点，作射线OC，OE平分∠AOC，OF平分∠BOC．
18．下列运算正确的是（ ）
| A． | $\sqrt{18}$$-\sqrt{2}$=2 | B． | $\sqrt{14}$×$\sqrt{2}$=2$\sqrt{7}$ | C． | （$\sqrt{3}+2）$2=7 | D． | （-2ab2）3=-6a3b6 |