题目内容
3.分解因式:(1)x6+64y6;
(2)x6-64y6;
(3)8x3+27y3+36x2y+54xy2;
(4)64x6-48x4+12x2-1.
分析 根据因式分解的方法-分组分解法分解即可得到结论.
解答 解:(1)x6+64y6
=(x2+4y2)(x4-4x2y2+16y4);
(2)x6-64y6
=(x2-4y2)(x4-4x2y2+16y4)
=(x+2y(x-2y)(x4-4x2y2+y4);
(3)8x3+27y3+36x2y+54xy2
=(2x+3y)(4x2-6xy+9y2)+18xy(2x+3y)
=(2x+3y)(4x2+12xy+9y2)
=(2x+3y)(2x+3y)2
=(2x+3y)3;
(4)64x6-48x4+12x2-1
=(64x6-1)-(48x4-12x2)
=(4x2-1)(16x4+4x2+1)-12x2(4x2-1)
=(4x2-1)(16x4+4x2+1-12x2)
=(4x2-1)(16x4-8x2+1)
=(4x2-1)3
=(2x+1)3(2x-1)3.
点评 本题考查了分组分解法分解因式,熟练掌握分组分解法是解题的关键.

练习册系列答案
相关题目
14.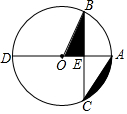 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )| A. | $\frac{8}{9}π-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{8}{9}π-\frac{{4\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{18}π-\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{16}{9}π-\frac{{2\sqrt{3}}}{3}$ |
18.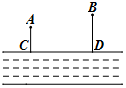 如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
 如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )| A. | 距C点1km处 | B. | 距C点2km处 | C. | 距C点3km处 | D. | CD的中点处 |
13.小芳和小丽是乒乓球运动员,在一次比赛中,每人只允许保“双打”或“单打”中的一项,那么两人同时报单打的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.
我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.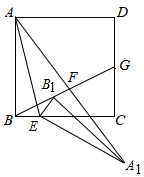 如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;