题目内容
19.食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂0.4克,B饮料每瓶需加该添加剂0.5克,已知生产A、B两种饮料共100瓶恰好用了这种添加剂共46克.(1)A、B两种饮料各生产了多少瓶?
(2)若该饮料加工厂想利用现有库存的102kg这种食品添加剂生产A、B两种饮料共10000箱(每箱24瓶),且根据市场营销情况,B种饮料的生产数量不少于A中饮料的$\frac{1}{4}$,该饮料加工厂应如何安排两种饮料的生产数量?
分析 (1)设A种饮料生产了x瓶、B种饮料生产了y瓶,根据“A、B两种饮料共100瓶、用了这种添加剂共46克”列二元一次方程组求解可得;
(2)设该饮料加工厂安排生产A种饮料m瓶,则安排生产B种饮料(240000-m)瓶,根据“所用添加剂不超过102kg、B种饮料的生产数量不少于A中饮料的$\frac{1}{4}$”列一元一次不等式组求解可得.
解答 解:(1)设A种饮料生产了x瓶、B种饮料生产了y瓶,
根据题意,得:$\left\{\begin{array}{l}{x+y=100}\\{0.4x+0.5y=46}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=60}\end{array}\right.$,
答:A种饮料生产了40瓶、B种饮料生产了50瓶;
(2)设该饮料加工厂安排生产A种饮料m瓶,则安排生产B种饮料(240000-m)瓶,
由题意,得:$\left\{\begin{array}{l}{240000-m≥\frac{1}{4}m}\\{0.4m+0.5(240000-m)≤102000}\end{array}\right.$,
解得:180000≤m≤192000,
即该饮料加工厂安排生产A种饮料的箱数不少于7500箱、不高于8000箱;
该饮料加工厂安排生产B种饮料的箱数不少于2000箱、不高于2500箱.
点评 本题主要考查二元一次方程组和一元一次不等式组的应用,理解题意找到题目蕴含的相等关系或不等关系列出方程组和不等式组是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
7.下列分式是最简分式的是( )
| A. | $\frac{x-y}{{{x^2}+{y^2}}}$ | B. | $\frac{xy-y}{3xy}$ | C. | $\frac{m-1}{1-m}$ | D. | $-\frac{61m}{32m}$ |
14.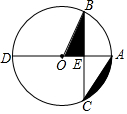 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )| A. | $\frac{8}{9}π-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{8}{9}π-\frac{{4\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{18}π-\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{16}{9}π-\frac{{2\sqrt{3}}}{3}$ |
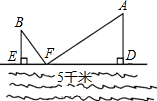 如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.
如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.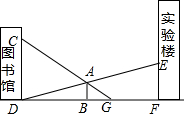 某中学的图书馆与实验楼中间有一地标牌AB,小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A,他们的视线如图所示,小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处,小夕从点E恰好可以看到图书馆的底部D处,已知图中的所有点均在同一平面内,CD⊥DF,AB⊥DF,EF⊥DF,CD=6米,EF=3米,DF=25米,请你根据以上数据,求该地标牌的高度AB及它与图书馆之间的距离BD(结果精确到0.1米).
某中学的图书馆与实验楼中间有一地标牌AB,小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A,他们的视线如图所示,小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处,小夕从点E恰好可以看到图书馆的底部D处,已知图中的所有点均在同一平面内,CD⊥DF,AB⊥DF,EF⊥DF,CD=6米,EF=3米,DF=25米,请你根据以上数据,求该地标牌的高度AB及它与图书馆之间的距离BD(结果精确到0.1米). 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.
我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.