题目内容
13.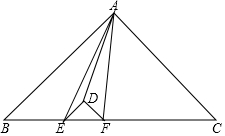 如图,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连接AE、AD、AF,于是整个图形被分成五块小三角形.其中三块的面积为S△DEF=1、S△ADE=2、S△ADF=3,那么△ABC的面积是36.
如图,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连接AE、AD、AF,于是整个图形被分成五块小三角形.其中三块的面积为S△DEF=1、S△ADE=2、S△ADF=3,那么△ABC的面积是36.
分析 如图连接BD、CD.由DE∥AB,DF∥AC,推出S△DEA=S△DEB=2,S△DFA=S△DFC=3,由S△EDF=1,可知S△BCD=1+2+3=6,推出EF:BC=1:6,由△DEF∽△ABC,可得$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=$\frac{1}{36}$,由此即可解决问题.
解答 解: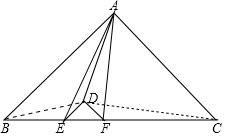 如图连接BD、CD.
如图连接BD、CD.
∵△ABC,△EDF都是等腰直角三角形,
∴∠DEF=∠ABC=45°,∠DFE=∠AC=45°,
∴DE∥AB,DF∥AC,
∴S△DEA=S△DEB=2,S△DFA=S△DFC=3,
∵S△EDF=1,
∴S△BCD=1+2+3=6,
∴EF:BC=1:6,
∵△DEF∽△ABC,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=$\frac{1}{36}$,
∴S△ABC=36.
故答案为36.
点评 本题考查等腰直角三角形的性质、平行线的判定和性质、相似三角形的性质等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
7.下列分式是最简分式的是( )
| A. | $\frac{x-y}{{{x^2}+{y^2}}}$ | B. | $\frac{xy-y}{3xy}$ | C. | $\frac{m-1}{1-m}$ | D. | $-\frac{61m}{32m}$ |
 如图,直角三角尺的直角顶点在直线b上,∠3=25°,转动直线a,当∠1=65°时,a∥b.
如图,直角三角尺的直角顶点在直线b上,∠3=25°,转动直线a,当∠1=65°时,a∥b. 如图是某建筑物的屋顶架,其中AB=8m,D是AB的中点,BC,DE都垂直于AC.如果∠ABC=60°,那么BC,DE,CD各是多少米?
如图是某建筑物的屋顶架,其中AB=8m,D是AB的中点,BC,DE都垂直于AC.如果∠ABC=60°,那么BC,DE,CD各是多少米?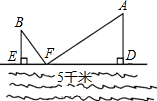 如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.
如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.