题目内容
17.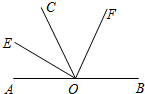 如图,O为直线AB上一点,作射线OC,OE平分∠AOC,OF平分∠BOC.
如图,O为直线AB上一点,作射线OC,OE平分∠AOC,OF平分∠BOC.(1)试判断OE与OF的位置关系,并说明理由;
(2)若∠COF:∠EOB=2:5,求∠AOF的度数.
分析 (1)由角平分线的定义知∠AOE=∠COE=$\frac{1}{2}$∠AOC、∠BOF=∠COF=$\frac{1}{2}$∠BOC,根据∠EOF=∠COE+∠COF=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)=90°可得答案;
(2)设∠BOF=∠COF=2x,则∠EOB=5x、∠BOC=4x,∠AOE=∠COE=∠BOE-∠BOC=x,根据∠AOC+∠BOC=180°求得x的值,由∠AOF=180°-∠BOF可得答案.
解答 解:(1)OE⊥OF,
∵OE平分∠AOC,OF平分∠BOC,
∴∠AOE=∠COE=$\frac{1}{2}$∠AOC、∠BOF=∠COF=$\frac{1}{2}$∠BOC,
∵∠AOC+∠BOC=180°,
∴∠EOF=∠COE+∠COF=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)=90°,
∴OE⊥OF;
(2)设∠BOF=∠COF=2x,则∠EOB=5x,∠BOC=4x,
∴∠AOE=∠COE=∠BOE-∠BOC=x,
∵∠AOC+∠BOC=180°,
∴2x+4x=180,
解得:x=30,
则∠AOF=180°-∠BOF=180°-2x=120°.
点评 本题主要考查角的计算和角平分线的定义,熟练掌握角平分线的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列分式是最简分式的是( )
| A. | $\frac{x-y}{{{x^2}+{y^2}}}$ | B. | $\frac{xy-y}{3xy}$ | C. | $\frac{m-1}{1-m}$ | D. | $-\frac{61m}{32m}$ |
5.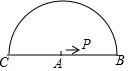 如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
 如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )| A. | 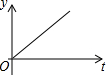 | B. | 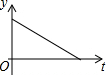 | C. | 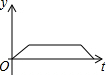 | D. | 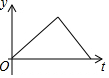 |
6.下列图形中,不属于轴对称图形的是( )
| A. | 等边三角形 | B. | 圆 | C. | 平行四边形 | D. | 矩形 |
7.如果$\sqrt{4-x}$有意义,则x的取值范围是( )
| A. | x≥0 | B. | x≤0 | C. | x≥4 | D. | x≤4 |
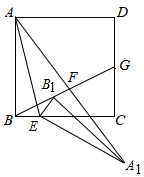 如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1; 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.