题目内容
20.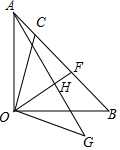 如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.
如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.
分析 如图,延长OF到M,使得OF=FM,连接CM,BM.只要证明△AOG≌△OBM,可得∠1=∠2,由∠1+∠3=90°,即可推出∠2+∠3=90°,即∠OHG=90°.
解答 证明:如图,延长OF到M,使得OF=FM,连接CM,BM.
∵FC=FB,OF=FM,
∴四边形OCMB是平行四边形,
∴OC=BM=OG,OC∥BM,
∴∠CBM=∠OCB=∠OAB+∠AOC,
∴∠OBM=OBA+∠CBM=∠OAB+∠AOC=90°+∠AOC,
∵∠AOG=90°+∠AOC,
∴∠AOG=∠OBM,
∵OA=OB,OG=BM,
∴△AOG≌△OBM,
∴∠1=∠2,
∵∠1+∠3=90°,
∴∠2+∠3=90°,
∴∠OHG=90°,
∴OH⊥AG.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
5.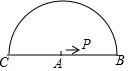 如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
 如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )| A. | 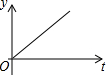 | B. | 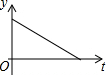 | C. | 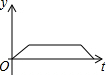 | D. | 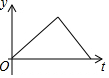 |
10.小涵将如图1所示学习桌的桌面抽象成了如图2所示的多边形,则图2中∠A+∠B+∠C+∠D+∠E+∠F等于( )
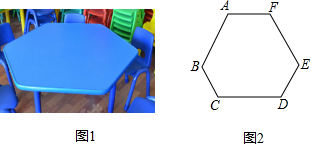

| A. | 640° | B. | 1080° | C. | 900° | D. | 720° |
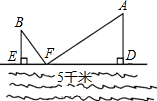 如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.
如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米. 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.
我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.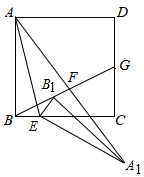 如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1; 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的取值范围.