题目内容
18.作图题(不写作法,保留作图痕迹):(1)尺规作图:校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P(如图1).(不写画图过程,保留作图痕迹)
(2)用直尺和圆规在如图2所示的数轴上作出表示$\sqrt{10}$的点.
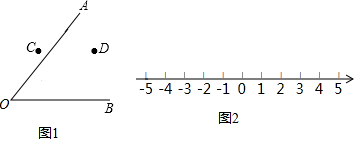
分析 (1)分别作线段CD的垂直平分线和∠AOB的角平分线,它们的交点即为点P;
(2)过3对应的点B作数轴的垂线l,再l上截取BC=1,则以原点为圆心,OC为半径画弧交数轴的正半轴于点A,则点A为所作.
解答 解;(1)如图1,点P为所作;
(2)如图2,点A表示的数为$\sqrt{10}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
8.下列说法中,错误的是( )
| A. | 4的算术平方根是±2 | B. | $\sqrt{81}$的平方根是±3 | ||
| C. | 8的立方根是2 | D. | 立方根等于-1的实数是-1 |
10. 已知二次函数y=x2+2x-3.
已知二次函数y=x2+2x-3.
(1)把函数配成y=a(x-h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
(4)当y>0时,则x的取值范围为x<-3或x>1.
(5)当-3<x<0时,则y的取值范围为-4≤y<0.
 已知二次函数y=x2+2x-3.
已知二次函数y=x2+2x-3.(1)把函数配成y=a(x-h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
| x | … | … | |||||
| y | … | … |
(5)当-3<x<0时,则y的取值范围为-4≤y<0.
8.已知|x|=4,|y|=$\frac{1}{2}$,且x<y,则$\frac{x}{y}$的值等于( )
| A. | 8 | B. | ±8 | C. | -8 | D. | -$\frac{1}{8}$ |
 如图,在正方形ABCD中,E、F分别是AB、BC的中点,点G是线段DE上一点,且∠EGF=45°,若AB=10,则DG=$\sqrt{5}$.
如图,在正方形ABCD中,E、F分别是AB、BC的中点,点G是线段DE上一点,且∠EGF=45°,若AB=10,则DG=$\sqrt{5}$.