题目内容
已知抛物线y=3ax2+2bx+c
(1)若a=b=1,c=-1,求该抛物线与x轴的交点坐标;
(2)若a=
,c=b-2,证明抛物线与x轴有两个交点;
(3)若a=
,c=2+b且抛物线在-2≤x≤2区间上的最小值是-3,求b的值.
(1)若a=b=1,c=-1,求该抛物线与x轴的交点坐标;
(2)若a=
| 1 |
| 3 |
(3)若a=
| 1 |
| 3 |
考点:抛物线与x轴的交点,二次函数的最值
专题:
分析:(1)将a、b、c的值代入,可得出抛物线解析式,从而可求解抛物线与x轴的交点坐标;
(2)把a=
,c=b-2代入抛物线解析式,表示出方程的判别式的表达式,利用配方法及完全平方的非负性即可判断出结论;
(3)a=
,c-b=2,则抛物线可化为y=x2+2bx+b+2,其对称轴为x=-b,分x=-b<-1,x=-b>2两种情况讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.
(2)把a=
| 1 |
| 3 |
(3)a=
| 1 |
| 3 |
解答:(1)解:当a=b=1,c=-1,时,抛物线为y=3x2+2x-1,
∵方程3x2+2x-1=0的两个根为x1=-1,x2=
,
∴该抛物线与x轴交点的坐标是(-1,0)和(
,0);
(2)证明:当a=
,c=b-2时,抛物线y=x2+2bx+b-2,设y=0,则x2+2bx+b-2=0,
∴△=4b2-4b+8=(2b-1)2+7>0,
∴抛物线与x轴有两个交点;
(3)解:a=
,c-b=2,则抛物线可化为y=x2+2bx+b+2,其对称轴为x=-b,
当x=-b<-1时,即b>1,则有抛物线在x=-1时取最小值为-3,
此时-3=(-1)2+2×(-1)b+b+2,
解得:b=6,符合题意;
当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,
此时-3=22+2×2b+b+2,
解得:b=-
,不合题意,舍去.
当-1≤-b≤2时,即-2≤b≤1,则有抛物线在x=-b时取最小值为-3,
此时-3=(-b)2+2×(-b)b+b+2,
化简得:b2-b-5=0,
解得:b=
(不合题意,舍去),b=
,
综上可得:b=6或b=
.
∵方程3x2+2x-1=0的两个根为x1=-1,x2=
| 1 |
| 3 |
∴该抛物线与x轴交点的坐标是(-1,0)和(
| 1 |
| 3 |
(2)证明:当a=
| 1 |
| 3 |
∴△=4b2-4b+8=(2b-1)2+7>0,
∴抛物线与x轴有两个交点;
(3)解:a=
| 1 |
| 3 |
当x=-b<-1时,即b>1,则有抛物线在x=-1时取最小值为-3,
此时-3=(-1)2+2×(-1)b+b+2,
解得:b=6,符合题意;
当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,
此时-3=22+2×2b+b+2,
解得:b=-
| 9 |
| 5 |
当-1≤-b≤2时,即-2≤b≤1,则有抛物线在x=-b时取最小值为-3,
此时-3=(-b)2+2×(-b)b+b+2,
化简得:b2-b-5=0,
解得:b=
1+
| ||
| 2 |
1-
| ||
| 2 |
综上可得:b=6或b=
1-
| ||
| 2 |
点评:本题考查了二次函数的综合,涉及了一元二次方程的解,求根公式及根与系数的关系,解答本题的难点在第三问,关键是分类讨论,此题难度较大.

练习册系列答案
相关题目
 如图,已知AB是⊙O的直径,则∠A=35°,则∠B=( )
如图,已知AB是⊙O的直径,则∠A=35°,则∠B=( )| A、55° | B、65° |
| C、45° | D、75° |
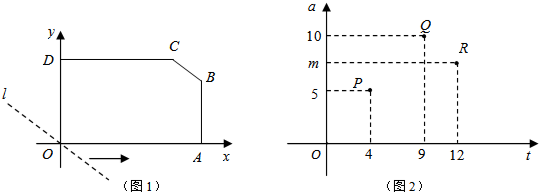
 如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=

 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,点B在⊙O上,BP的延长线交直线l于点C,连结AB,AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,点B在⊙O上,BP的延长线交直线l于点C,连结AB,AB=AC. 我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.
我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.