题目内容
 我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.
我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.(1)求a的值.
(2)点C(-1,n)是抛物线上一点,点C关于原点O的对称点为D,连接CD、BD、BC,求△BCD的面积.
考点:二次函数的应用
专题:
分析:(1)直接将(4,0)代入y=ax2+4求出a即可;
(2)首先过点C作CE⊥AB于点E,DF⊥AB于点F,进而求出C点坐标,即可得出D点坐标,再利用S△BCD=S△BOD+S△BOC求出即可.
(2)首先过点C作CE⊥AB于点E,DF⊥AB于点F,进而求出C点坐标,即可得出D点坐标,再利用S△BCD=S△BOD+S△BOC求出即可.
解答: 解:(1)由题意得:A(-4,0),B(4,0),
解:(1)由题意得:A(-4,0),B(4,0),
代入抛物线解析式得:a×42+4=0,
解得:a=-
;
(2)过点C作CE⊥AB于点E,DF⊥AB于点F,
由(1)知抛物线解析式是y=-
x2+4,
∴令x=-1,得y=-
×(-1)2+4=
,
∴C(-1,
),
∵点C关于原点O对称的点为D,
∴D(1,-
),
∴S△BCD=S△BOD+S△BOC
=
×4×
+
×4×
=15(m2).
 解:(1)由题意得:A(-4,0),B(4,0),
解:(1)由题意得:A(-4,0),B(4,0),代入抛物线解析式得:a×42+4=0,
解得:a=-
| 1 |
| 4 |
(2)过点C作CE⊥AB于点E,DF⊥AB于点F,
由(1)知抛物线解析式是y=-
| 1 |
| 4 |
∴令x=-1,得y=-
| 1 |
| 4 |
| 15 |
| 4 |
∴C(-1,
| 15 |
| 4 |
∵点C关于原点O对称的点为D,
∴D(1,-
| 15 |
| 4 |
∴S△BCD=S△BOD+S△BOC
=
| 1 |
| 2 |
| 15 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
=15(m2).
点评:此题主要考查了二次函数的应用以及三角形面积求法和关于原点对称点的坐标性质等知识,得出D点坐标是解题关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,直线y=-
如图,直线y=-
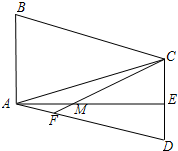 已知:在?ABCD中,AE⊥CD,垂足为E,点M为AE上一点,且ME=AB,AM=CE,连接CM并延长交AD于点F.
已知:在?ABCD中,AE⊥CD,垂足为E,点M为AE上一点,且ME=AB,AM=CE,连接CM并延长交AD于点F. 如图,以等腰直角△ABC两锐角顶点A、B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为
如图,以等腰直角△ABC两锐角顶点A、B为圆心作等圆,⊙A与⊙B恰好外切,若AC=2,那么图中两个扇形(即阴影部分)的面积之和为 如图,直角三角形ABO放置在平面直角坐标系中,已知斜边OA在x轴正半轴上,且OA=4,AB=2,将该三角形绕着点O逆时针旋转120°后点B的对应点恰好落在一反比例函数图象上,则该反比例函数的解析式为
如图,直角三角形ABO放置在平面直角坐标系中,已知斜边OA在x轴正半轴上,且OA=4,AB=2,将该三角形绕着点O逆时针旋转120°后点B的对应点恰好落在一反比例函数图象上,则该反比例函数的解析式为