题目内容
 如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=| a |
| x |
(1)分别求直线l和双曲线的解析式;
(2)若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)设直线l的解析式是y=kx+b,把C(4,1)、D(1,4)两点的坐标代入函数的解析式,即可求出答案;
(2)设直线l平移后的解析式为y=-x+5-m,组成方程组
,整理得出方程-x2+(5-m)x-4=0,得出△=(5-m)2-4×(-1)×(-4)=0,求出即可.
(2)设直线l平移后的解析式为y=-x+5-m,组成方程组
|
解答:解:(1)设直线l的解析式是y=kx+b,
∵直线l和反比例函数y=
交于C(4,1)、D(1,4)两点,
∴a=4,
,
解得:k=-1,b=5.
∴直线l的解析式为y=-x+5,双曲线的解析式是y=
;
(2)设直线l平移后的解析式为y=-x+5-m,
则
,
整理得:-x2+(5-m)x-4=0,
∵直线与双曲线有且只有一个交点,
∴△=(5-m)2-4×(-1)×(-4)=0,
∴m=1或9,
∵x>0,
∴m=1,
即当m=1时,直线与双曲线有且只有一个交点.
∵直线l和反比例函数y=
| a |
| x |
∴a=4,
|
解得:k=-1,b=5.
∴直线l的解析式为y=-x+5,双曲线的解析式是y=
| 4 |
| x |
(2)设直线l平移后的解析式为y=-x+5-m,
则
|
整理得:-x2+(5-m)x-4=0,
∵直线与双曲线有且只有一个交点,
∴△=(5-m)2-4×(-1)×(-4)=0,
∴m=1或9,
∵x>0,
∴m=1,
即当m=1时,直线与双曲线有且只有一个交点.
点评:本题考查了一次函数和反比例函数的交点问题,平移的性质,根的判别式,用待定系数法求一次函数的解析式的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
若m>n,则下列不等式成立的是( )
| A、-3m>-2n |
| B、am>an |
| C、a2m>a2n |
| D、m-2>n-3 |
 公园计划砌一个形状如图1的喷水池,后来有人建议改为图2的形状,且外圆直径不变,请比较图1的周长L1,与图2中四个圆周长的和L2的大小,正确的是( )
公园计划砌一个形状如图1的喷水池,后来有人建议改为图2的形状,且外圆直径不变,请比较图1的周长L1,与图2中四个圆周长的和L2的大小,正确的是( )| A、L1>L2 |
| B、L1=L2 |
| C、L1<L2 |
| D、大小不确定 |
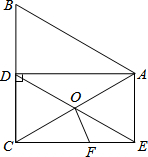 如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD. △ABC中,D是BC的中点.分别以AB,AC为一边,向三角形内部作Rt△ABE,Rt△ACF,使∠ABE=∠ACF,连接DE,DF,求证:DE=DF.
△ABC中,D是BC的中点.分别以AB,AC为一边,向三角形内部作Rt△ABE,Rt△ACF,使∠ABE=∠ACF,连接DE,DF,求证:DE=DF.