题目内容
如图1,A、D分别在x轴和y轴上,CD∥x轴,AB∥y轴.直线l:y=kx从点O出发,以1cm/s的速度沿x轴正方向运动,依次经过点D、A.记直线l被五边形OABCD截得的线段长度为a cm,直线l运动的时间为t s,a与t之间的函数图象是由3条线段组成,P(4,5)、Q(9,10)、R(12,m)依次分别为三段函数图象上的一点,如图2所示.当t=16时,直线l与BC重合,此时a=
.
(1)求当t=4时直线l的解析式;
(2)求m的值;
(3)若直线l将五边形分成周长为12:19的两部分,求t的值.
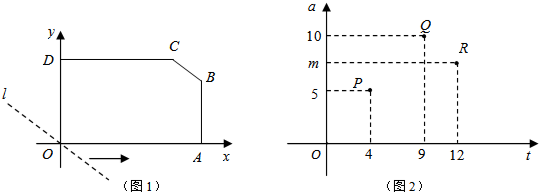
| 5 |
| 2 |
(1)求当t=4时直线l的解析式;
(2)求m的值;
(3)若直线l将五边形分成周长为12:19的两部分,求t的值.
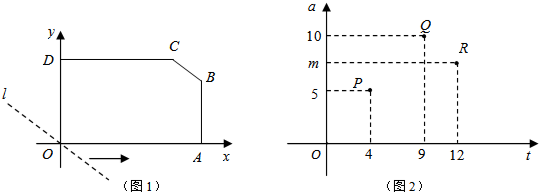
考点:一次函数综合题
专题:
分析:(1)当t=4时,求得直线l与x轴的交点M坐标,然后根据勾股定理求得直线与y轴的交点,利用待定系数法即可求得直线的解析式;
(2)根据Q在a与t之间的函数图象的第二段上,此段函数应该是与x轴平行的线段,当直线l经过D点时,解得的线段的长是10,根据勾股定理即可求得OD的长,从而求得C的纵坐标,然后延长DC、AB交于点G,在直角△BCG中,求得CG的长度,即可求得A的坐标,和AB的长,则当t=12时,即可求解;
(3)分直线在过D的直线左边和右边两种情况进行讨论,用t表示出直线l左边部分的长度,然后根据12:19的两部分,再分两种情况讨论求解.
(2)根据Q在a与t之间的函数图象的第二段上,此段函数应该是与x轴平行的线段,当直线l经过D点时,解得的线段的长是10,根据勾股定理即可求得OD的长,从而求得C的纵坐标,然后延长DC、AB交于点G,在直角△BCG中,求得CG的长度,即可求得A的坐标,和AB的长,则当t=12时,即可求解;
(3)分直线在过D的直线左边和右边两种情况进行讨论,用t表示出直线l左边部分的长度,然后根据12:19的两部分,再分两种情况讨论求解.
解答:解:(1)当t=4时,直线l与x轴的交点M坐标是(4,0),
MN=5,则ON=
=
=3,
则N的坐标是(0,3).
设直线l的解析式是y=kx+b,则
,
解得:
,

则直线的解析式是:y=-
x+3;
(2)设OD=m,则当直线经过点D时,直线l的解析式是y=-
x+m,令y=0,解得:x=
m,
则
=10,
解得:m=6,
则OD=6,C的纵坐标是6,
设直线当移动到BC的位置时,直线的解析式是y=-
x+b,
直线与x轴的交点坐标是(16,0),
则-12+b=0,
解得:b=12,
则直线的解析式是:y=-
x+12,
令y=6,得到:-
x+12=6,
解得:x=8.
即C的横坐标是8.C的坐标是(8,6).
延长DC、AB交于点G.则
=
,
设BG=3x,则CG=4x,
则(3x)2+(4x)2=(
)2,
解得:x=
,
则CG=2,BG=
,
则OA=8+2=10,
则当t=12时,设直线交x轴于点E,交AB于点F.
则AE=2,
则AF=
×2=
,
则EF=
=
.
即:m=
;
(3)AB=6-BG=6-
=
,
则五边形OABGD的周长是:10+
+
+8+6=31.
当直线经过点D时,t=8,
当0<t≤8时,若t+
t=
×31,解得:t=
,
若t+
t=
×31,解得:t=
(舍去);
当8<t<16时,当t+6+(t-8)=
×31,解得:t=7(舍去),
当t+6+(t-8)=
×31,解得:t=
(舍去).
总之,t=
或
.
MN=5,则ON=
| MN2-OM2 |
| 52-42 |
则N的坐标是(0,3).
设直线l的解析式是y=kx+b,则
|
解得:
|

则直线的解析式是:y=-
| 3 |
| 4 |
(2)设OD=m,则当直线经过点D时,直线l的解析式是y=-
| 3 |
| 4 |
| 4 |
| 3 |
则
m2+(
|
解得:m=6,
则OD=6,C的纵坐标是6,
设直线当移动到BC的位置时,直线的解析式是y=-
| 3 |
| 4 |
直线与x轴的交点坐标是(16,0),
则-12+b=0,
解得:b=12,
则直线的解析式是:y=-
| 3 |
| 4 |
令y=6,得到:-
| 3 |
| 4 |
解得:x=8.
即C的横坐标是8.C的坐标是(8,6).
延长DC、AB交于点G.则
| BG |
| CG |
| 3 |
| 4 |
设BG=3x,则CG=4x,
则(3x)2+(4x)2=(
| 5 |
| 2 |
解得:x=
| 1 |
| 2 |
则CG=2,BG=
| 3 |
| 2 |
则OA=8+2=10,
则当t=12时,设直线交x轴于点E,交AB于点F.

则AE=2,
则AF=
| 3 |
| 4 |
| 3 |
| 2 |
则EF=
22+(
|
| 5 |
| 2 |
即:m=
| 15 |
| 2 |
(3)AB=6-BG=6-
| 3 |
| 2 |
| 9 |
| 2 |
则五边形OABGD的周长是:10+
| 9 |
| 2 |
| 5 |
| 2 |
当直线经过点D时,t=8,
当0<t≤8时,若t+
| 3 |
| 4 |
| 12 |
| 12+19 |
| 48 |
| 7 |
若t+
| 3 |
| 4 |
| 19 |
| 12+19 |
| 74 |
| 7 |
当8<t<16时,当t+6+(t-8)=
| 12 |
| 12+19 |
当t+6+(t-8)=
| 19 |
| 12+19 |
| 74 |
| 7 |
总之,t=
| 48 |
| 7 |
| 74 |
| 7 |
点评:本题是一次函数与勾股定理,相似三角形的性质的综合应用,正确求得OA,AB的长是关键.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
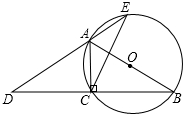 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE. 如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,
如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0, 如图,用长30cm,宽25cm的长方形地板砖30块摆成一个正方形地面,这块正方形地面的边长是多少?
如图,用长30cm,宽25cm的长方形地板砖30块摆成一个正方形地面,这块正方形地面的边长是多少?