��Ŀ����
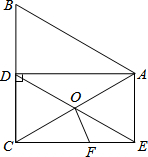
��ͼ��������ABCD�У�AD��BC����ABC=45�㣬AB=4
��AD=7��BC=14������E�ӵ�B��������B-C������2cm/s���ٶ��˶���ͬʱ����F�ӵ�C��������C-D-A��2cm/s���ٶ��˶�������E��MEBC��������B-A-D�ཻ�ڵ�M������M���D�غ�ʱ���������㶼ֹͣ�˶������E��F�˶���ʱ��Ϊt�루t��0�����ɵ�B��M��E��F��ɵ��ı��ε����ΪS��
��1�����߶�CD�ij���
��2���Ƿ���ں��ʵ�t��ʹ�á�EFM�ǵ��������Σ��������ڣ���˵�����ɣ������ڣ������Ӧ��t��ֵ��
��3��ֱ��д��S��t�ĺ�����ϵʽ����Ӧ��t��ȡֵ��Χ��

| 2 |
��1�����߶�CD�ij���
��2���Ƿ���ں��ʵ�t��ʹ�á�EFM�ǵ��������Σ��������ڣ���˵�����ɣ������ڣ������Ӧ��t��ֵ��
��3��ֱ��д��S��t�ĺ�����ϵʽ����Ӧ��t��ȡֵ��Χ��

���㣺�ı����ۺ���
ר�⣺
��������1����ͼ1����AE��BC��E��DF��BC��F���ɹ��ɶ����Ϳ������AE��DF��ֵ���������CD��ֵ��
��2����ͼ3����ͼ4�����ݣ�1���Ľ������tan��B=
=1��sin��C=
=
��cos��C=
���ɵ��������εķ������۾Ϳ������t��ֵ��
��3����ͼ5��6��7��8����4�������0��t��2ʱ��2��t��2.5��2.5��t��4��4��t��5.5ʱ���������ε������ʽ�����ε������ʽ�Ϳ��Ա�ʾ��S��t�Ĺ�ϵʽ��
��2����ͼ3����ͼ4�����ݣ�1���Ľ������tan��B=
| AE |
| BE |
| DF |
| CD |
| 4 |
| 5 |
| 3 |
| 5 |
��3����ͼ5��6��7��8����4�������0��t��2ʱ��2��t��2.5��2.5��t��4��4��t��5.5ʱ���������ε������ʽ�����ε������ʽ�Ϳ��Ա�ʾ��S��t�Ĺ�ϵʽ��
����⣺��1����ͼ1����AE��BC��E��DF��BC��F��
���AEB=��AEF=��DFC=��DFE=90�㣮
�ߡ�ABC=45�㣬
���BAE=45�㣬
���ABC=��BAE��
��AE=BE��
��Rt��ABE��AB=4
���ɹ��ɶ�������
BE=AE=4��
��AD��BC��
���DAE=��AEB=90�㣮
���AEF=��EAD=��DFE=90�㣬
���ı���AEFD�Ǿ��Σ�
��AD=EF��AE=DF��
��DF=4��
��AD=7��
��EF=7��
��BC=14��
��CF=14-7-4=3
��Rt��DFC�й��ɶ�������
CD=5��
��CD�ij�Ϊ5��
��2���ߡ�AEB=��DFC=90�㣬
��tan��B=
=1��sin��C=
=
��cos��C=
��
��ͼ2����MF=EFʱ����FH��EM��H��FG��BC��G��
���FHE=��FGE=90�㣬��MEC=90��
���ı���HEGF�Ǿ��Σ�
��HE=GF��
��EH=
EM=
BE=t��GF=
t��
��t=
t��
��t=0����ȥ����
��ͼ3����MF=MEʱ����AG��BC��BC��G��
��AM=2t-4��
��FD=2t-5��
��MF=7-��2t-4��-��2t-5��=16-4t��
��16-4t=4��
��t=3��
��ͼ4����MF=MEʱ����AG��BC��BC��G��
��AM=2t-4��
��AF=12-2t��
��MF=AM-AF=2t-4-��12-2t��=4t-16��
��4t-16=4��
��t=5��
��t=3��t=4ʱ����EFM�ǵ��������Σ�
��3����ͼ5����0��t��2ʱ����FG��BC��G��
���FGC=90�㣬
��FG=
t��CG=
t��
��BE=EM=2t��
��EG=14-2t-
t=14-
t��
��S=
+
=2t2+14t-
t2=-
t2+14t��
��ͼ6����2��t��2.5ʱ����FG��BC��G��
S=
+
=28-
t��
��ͼ7����2.5��t��4ʱ��
S=
=
=-4t+32��
��ͼ8��4��t��5.5ʱ��
S�T
=
=12t-32��
��S=
��
���AEB=��AEF=��DFC=��DFE=90�㣮

�ߡ�ABC=45�㣬
���BAE=45�㣬
���ABC=��BAE��
��AE=BE��
��Rt��ABE��AB=4
| 2 |
BE=AE=4��
��AD��BC��
���DAE=��AEB=90�㣮

���AEF=��EAD=��DFE=90�㣬
���ı���AEFD�Ǿ��Σ�
��AD=EF��AE=DF��
��DF=4��
��AD=7��
��EF=7��
��BC=14��
��CF=14-7-4=3

��Rt��DFC�й��ɶ�������
CD=5��
��CD�ij�Ϊ5��
��2���ߡ�AEB=��DFC=90�㣬
��tan��B=
| AE |
| BE |
| DF |
| CD |
| 4 |
| 5 |
| 3 |
| 5 |
��ͼ2����MF=EFʱ����FH��EM��H��FG��BC��G��
���FHE=��FGE=90�㣬��MEC=90��
���ı���HEGF�Ǿ��Σ�
��HE=GF��
��EH=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
��t=
| 8 |
| 5 |
��t=0����ȥ����
��ͼ3����MF=MEʱ����AG��BC��BC��G��
��AM=2t-4��
��FD=2t-5��
��MF=7-��2t-4��-��2t-5��=16-4t��
��16-4t=4��
��t=3��
��ͼ4����MF=MEʱ����AG��BC��BC��G��
��AM=2t-4��
��AF=12-2t��
��MF=AM-AF=2t-4-��12-2t��=4t-16��
��4t-16=4��
��t=5��
��t=3��t=4ʱ����EFM�ǵ��������Σ�

��3����ͼ5����0��t��2ʱ����FG��BC��G��
���FGC=90�㣬
��FG=
| 8 |
| 5 |
| 6 |
| 5 |
��BE=EM=2t��
��EG=14-2t-
| 6 |
| 5 |
| 16 |
| 5 |
��S=
| 2t��2t |
| 2 |
2t(14-
| ||
| 2 |
| 16 |
| 5 |
| 6 |
| 5 |
��ͼ6����2��t��2.5ʱ����FG��BC��G��
S=
| 4��2t |
| 2 |
4(14-
| ||
| 2 |
| 12 |
| 5 |
��ͼ7����2.5��t��4ʱ��
S=
| ME(MF+BE) |
| 2 |
| 4(16-4t+2t) |
| 2 |
��ͼ8��4��t��5.5ʱ��
S�T
| ME(MF+BE) |
| 2 |
| 4(4t-16+2t) |
| 2 |
��S=
|
���������⿼�������ε����ʵ����ã����ɶ��������ã�ֱ�������ε����ʵ����ã����Ǻ���ֵ�����ã������ε������ʽ�����ã����ε������ʽ�����ã������Ľ���ʽ�����ã����ʱ�����Ľ���ʽ������������κ����ε������ʽ�ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
��m��n�������в���ʽ�������ǣ�������
| A��-3m��-2n |
| B��am��an |
| C��a2m��a2n |
| D��m-2��n-3 |
 ��ͼ���ڡ�ABC�У�AB=AC��ADƽ�֡�BAC��CE��AD��CE=AD��
��ͼ���ڡ�ABC�У�AB=AC��ADƽ�֡�BAC��CE��AD��CE=AD�� ��ABC�У�D��BC���е㣮�ֱ���AB��ACΪһ�ߣ����������ڲ���Rt��ABE��Rt��ACF��ʹ��ABE=��ACF������DE��DF����֤��DE=DF��
��ABC�У�D��BC���е㣮�ֱ���AB��ACΪһ�ߣ����������ڲ���Rt��ABE��Rt��ACF��ʹ��ABE=��ACF������DE��DF����֤��DE=DF��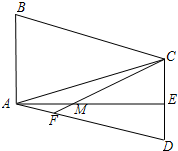 ��֪����?ABCD�У�AE��CD������ΪE����MΪAE��һ�㣬��ME=AB��AM=CE������CM���ӳ���AD�ڵ�F��
��֪����?ABCD�У�AE��CD������ΪE����MΪAE��һ�㣬��ME=AB��AM=CE������CM���ӳ���AD�ڵ�F��