题目内容
11. 如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )| A. | AM∥BN | B. | AM=BN | C. | BC=ML | D. | ∠ACB=∠MLN |
分析 根据平移的性质,对应点的连线互相平行且相等,平移变换只改变图形的位置不改变图形的形状与大小对各小题分析判断即可得解.
解答 解:∵△ABC沿着XY方向平移一定的距离得到△MNL,
∴①对应边相等:AB=MN,AC=ML,BC=NL,∴B正确,C错误;
②对应角相等:∠ABC=∠MNL,∠BCA=∠NLM,∠BAC=∠NML,∴D正确,
③对应点的连线互相平行且相等:平行AM∥BN∥CL,∴正确,
相等AM=BN=CL,
故选C
点评 次题是平移的性质,考查了平移的性质:对应线段相等,对应角相等,对应点的连线互相平行且相等,熟练掌握平移的性质是解本题的关键,注意:由平移的性质,对应点的连线互相平行,可以得到新的结论:同位角相等,内错角相等,同旁内角互补.

练习册系列答案
相关题目
1. 已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
①AG⊥BE;②∠DGE=60°;③BF=2FG;④AD+$\sqrt{2}$DC=AB.
其中正确的结论有( )
 已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:①AG⊥BE;②∠DGE=60°;③BF=2FG;④AD+$\sqrt{2}$DC=AB.
其中正确的结论有( )
| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
6.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )
| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
16.下列各组二次根式中,不能合并的是( )
| A. | $\sqrt{20}$和$\sqrt{5}$ | B. | $\sqrt{12}$和$\sqrt{27}$ | C. | $\sqrt{\frac{1}{3}}$或$\sqrt{\frac{2}{3}}$ | D. | $\sqrt{45a}$和$\sqrt{125a}$ |
3. 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )| A. | 60° | B. | 25° | C. | 35° | D. | 45° |
20.举反例说明“一个锐角的余角小于这个角”是假命题,下面错误的是( )
| A. | 设一个角是45°,它的余角是45°,但45°=45° | |
| B. | 设一个角是60°,它的余角是30°,但30°<60° | |
| C. | 设一个角是30°,它的余角是60°,但60°>30° | |
| D. | 设一个角是10°,它的余角是80°,但80°>10° |
1.若分式方程$\frac{x-3}{x-1}=\frac{m}{x-1}$有增根,则m等于( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
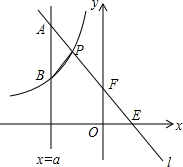 如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式.
如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式. 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.