题目内容
19. 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
分析 由四边形ABCD正方形,BF=BD=10$\sqrt{2}$,由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
解答 (1)解:∵在正方形ABCD中,∠BCD=90°,BC=CD=10,
∴BD=10$\sqrt{2}$.
∵DF⊥DE,
∴∠ADE+∠EDC=90°,∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{AD=DC}\\{∠A=∠DCF}\end{array}\right.$
∴△ADE≌△CDF(ASA),
∴AE=CF.
又∵BD=BF=10$\sqrt{2}$,
∴AE=CF=BF-BC=10$\sqrt{2}$-10,
∴BE=AB-AE=10-(10$\sqrt{2}$-10)=20-10$\sqrt{2}$,
即BE的长为20-10$\sqrt{2}$;
点评 此题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质.此题综合性较强,难度较大,注意数形结合思想的应用.

练习册系列答案
相关题目
10. 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
14. 如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )
如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )
 如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )
如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
11. 如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
 如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )| A. | AM∥BN | B. | AM=BN | C. | BC=ML | D. | ∠ACB=∠MLN |
8.下列各组线段中,能够组成直角三角形的一组是( )
| A. | 1cm,2cm,3cm | B. | 2cm,3cm,4cm | C. | 4cm,5cm,6cm | D. | 1cm,$\sqrt{2}$cm,$\sqrt{3}$cm |
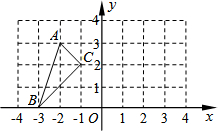 如图,△ABC的顶点都在方格线的交点(格点)上.
如图,△ABC的顶点都在方格线的交点(格点)上.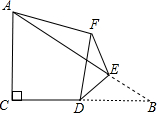 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为$\frac{12\sqrt{5}}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为$\frac{12\sqrt{5}}{5}$. 如图,在矩形ABCD中,E为AD的中点,∠BED的角平分线交BC于F.若AB=6,BC=16,则FC的长度为( )
如图,在矩形ABCD中,E为AD的中点,∠BED的角平分线交BC于F.若AB=6,BC=16,则FC的长度为( )