题目内容
2.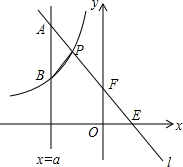 如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式.
如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式.
分析 首先求出点P坐标,再利用中点坐标公式求出k、b,分a<-1和a>-1两种情形讨论即可.
解答 解:把点P(-1,n)代入y=-$\frac{4}{x}$中,得到n=4,P(-1.4)
∵F(0,b),E(-$\frac{b}{k}$,0),F是PE中点,
∴$\left\{\begin{array}{l}{b=\frac{4+0}{2}}\\{0=\frac{-1-\frac{b}{k}}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴直线解析式为y=-2x+2,
∴当a<-1时,m=-2a+2-(-$\frac{4}{a}$)=-2a+$\frac{4}{a}$+2,
当a>-1时,m=-$\frac{4}{a}$-(-2a+2)=-$\frac{4}{a}$+2a-2.
点评 本题考查反比例函数与一次函数的交点问题、待定系数法等知识,解题的关键是灵活运用待定系数法解决问题,属于中考常考题型.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10. 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
14. 如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )
如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )
 如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )
如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
11. 如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
 如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )| A. | AM∥BN | B. | AM=BN | C. | BC=ML | D. | ∠ACB=∠MLN |
12.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 1,1,$\sqrt{2}$ | B. | 6,24,25 | C. | 6,8,10 | D. | 9,12,15 |
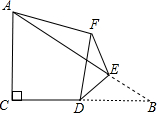 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为$\frac{12\sqrt{5}}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为$\frac{12\sqrt{5}}{5}$.