题目内容
1. 已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:①AG⊥BE;②∠DGE=60°;③BF=2FG;④AD+$\sqrt{2}$DC=AB.
其中正确的结论有( )
| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 延长ED交AB于M,证△ACD≌△BCE知∠ADC=∠BEC=75°,即可判断①;求得Rt△EDF中∠EDF=60°,知DE=2DF=2FG即DF=FG,结合AG⊥BE可判断②;在Rt△ACD中由∠ADC=75°可令CD=$\sqrt{6}-\sqrt{2}$、AC=$\sqrt{2}+\sqrt{6}$、AD=4,根据AB=$\sqrt{2}$AC,变形后可判断④;由DE=$\sqrt{2}$CD、FG=$\frac{1}{2}$DE、EF=$\frac{\sqrt{3}}{2}$DE可得FG、EF,再根据BF=BE-EF=AD-EF可得BF的长,即可判断③.
解答 解:如图,延长ED交AB于M,
则∠DMB=90°,
∵∠ADB=105°,△ABC是等腰直角三角形,
∴∠CDE=∠MDB=45°,∠ADC=75°,∠CAD=15°,
∴△DCE是等腰直角三角形,
∴CE=CD,
在△ACD和△BCE中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE=90°}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠ADC=∠BEC=75°,
∴∠AFE=180°-∠CAD-∠CEB=90°,即AF⊥BE,故①正确;
∵∠ADC=75°,∠CDE=45°,
∴Rt△EDF中,∠EDF=60°,
∴DE=2DF=2FG,即DF=FG,
∴EF垂直平分DG,
∴△DEG是等边三角形,
∴∠DGE=60°,故②正确;
方法一:在Rt△ACD中,∵∠ADC=75°,
∴∠PAD=15°,
作∠ADP=∠PAD=15°,
则PA=PD,∠CPD=30°,
设CD=a,则PD=PA=2a,PC=$\sqrt{3}$a,
∴AD=$\sqrt{C{D}^{2}+A{C}^{2}}$=$\sqrt{{a}^{2}+(2a+\sqrt{3}a)^{2}}$=$\sqrt{8+4\sqrt{3}}$a,
则$\frac{CD}{AD}$=$\frac{a}{\sqrt{8+4\sqrt{3}}a}$=$\sqrt{\frac{1}{8+4\sqrt{3}}}$=$\sqrt{\frac{8-4\sqrt{3}}{16}}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
同理可得$\frac{AC}{AD}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴CD:AC:AD=($\sqrt{6}-\sqrt{2}$):($\sqrt{6}+\sqrt{2}$):4,
∴令CD=$\sqrt{6}-\sqrt{2}$、AC=$\sqrt{2}+\sqrt{6}$、AD=4,
∴AB=$\sqrt{2}$AC=$\sqrt{2}$($\sqrt{2}+\sqrt{6}$)=2+2$\sqrt{3}$=4+$\sqrt{2}$($\sqrt{6}-\sqrt{2}$)=AD+$\sqrt{2}$CD,故④正确;
方法二:由①知∠AFB=90°,
∵∠ADC=∠BDF=75°,
∴∠DBF=15°,
由②知△DEG为等边三角形,且BE⊥AG,
∴DF=GF,
∴∠DBF=∠GBF=15°,
∴∠BGF=90°-∠GBF=75°,
∵∠ABG=∠ABD+∠DBF+∠GBF=75°,
∴AB=AG,
又∵DG=DE=$\sqrt{2}$CD,
∴AB=AG=AD+DG=AD+$\sqrt{2}$CD,故④正确;
∵DE=$\sqrt{2}$CD=$\sqrt{2}$($\sqrt{6}-\sqrt{2}$)=2$\sqrt{3}$-2,
∴FG=$\frac{1}{2}$DE=$\sqrt{3}$-1,EF=$\frac{\sqrt{3}}{2}$DE=3-$\sqrt{3}$,
∴BF=BE-EF=AD-EF=4-3+$\sqrt{3}$=1+$\sqrt{3}$,
显然BF≠2FG,故③错误;
综上可知,①②④正确,
故选:B.
点评 本题主要考查等腰直角三角形的性质、中垂线的性质、等边三角形的判定及角平分线定理等知识点,熟练掌握角平分线定理是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 了解某批灯泡的使用寿命情况 | B. | 了解全班同学每周体育锻炼的时间 | ||
| C. | 企业招聘,对应聘人员的面试 | D. | 对旅客上飞机的安检 |
 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
 如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )
如图所示,将△ABC沿着XY方向平移一定的距离得到△MNL,则下列结论中错误的是( )| A. | AM∥BN | B. | AM=BN | C. | BC=ML | D. | ∠ACB=∠MLN |
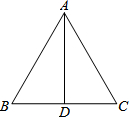 如图,在△ABC中,已知AB=AC,AD⊥BC于点D.请写出图中的等量关系,并说明等量关系成立的理由.
如图,在△ABC中,已知AB=AC,AD⊥BC于点D.请写出图中的等量关系,并说明等量关系成立的理由.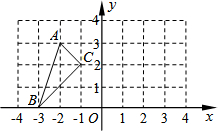 如图,△ABC的顶点都在方格线的交点(格点)上.
如图,△ABC的顶点都在方格线的交点(格点)上. 说理过程填空:
说理过程填空: