题目内容
8.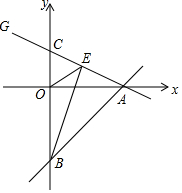 如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE.
如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE.(1)求∠OEB的度数;
(2)求点E的坐标.
分析 (1)根据已知条件得到△AOB是等腰直角三角形,求得∠OAB=45°,根据∠AOB=∠AEB=90°,得到B,O,E,A四点共圆,根据圆周角定理即可得到结论;
(2)设直线AC的解析式为y=kx+b,得到直线AC的解析式为y=-$\frac{1}{2}$x+2,由于BE⊥AC,得到直线BE的解析式为y=2x+4,解方程组即可得到结论.
解答 解:(1)在y=x-4中,当y=0时,x=4,当x=0时,y=4,
∴A(4,0),B(0,4),
∴△AOB是等腰直角三角形,
∴∠OAB=45°,
∵BE⊥AC,
∴∠AOB=∠AEB=90°,
∴B,O,E,A四点共圆,
∴∠OEB=∠OAB=45°;
(2)设直线AC的解析式为y=kx+b,
∵A(4,0),C(0,2),
∴$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{1}{2}$x+2,
∵BE⊥AC,
∴直线BE的解析式为y=2x-4,
解$\left\{\begin{array}{l}{y=2x-4}\\{y=-\frac{1}{2}x+2}\end{array}\right.$得,$\left\{\begin{array}{l}{x=\frac{12}{5}}\\{y=\frac{4}{5}}\end{array}\right.$,
∴E($\frac{12}{5}$,$\frac{4}{5}$).
点评 本题考查了一次函数图象上点的坐标特征,待定系数法求函数的解析式,等腰直角三角形的判定和性质,四点共圆,熟练掌握待定系数法求函数的解析式是解题的关键.

 阅读快车系列答案
阅读快车系列答案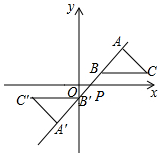 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3).
如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3).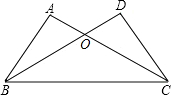 如图,△ABC与△DCB中,AC与BD交于点O,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点O,且∠A=∠D,AB=DC.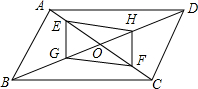 如图,?ABCD的对角线AC,BD交于点O,点E,F在AC上,点G,H在BD上,AF=CE,BH=DG,求证:GF∥HE.
如图,?ABCD的对角线AC,BD交于点O,点E,F在AC上,点G,H在BD上,AF=CE,BH=DG,求证:GF∥HE. 如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.
如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.