题目内容
20. 如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.
如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.
分析 首先证明四边形EBFD是平行四边形,则可得∠EBF=∠EDF,再根据等式的基本性质即可得到∠ABE=∠CDF.
解答 证明:
∵四边形ABCD是平行四边形,
∴AD∥BC,即ED=BF,∠ABC=∠ADC,
∵BE∥FD,
∴四边形EBFD是平行四边形,
∴∠EBF=∠EDF,
∴∠EBF-∠ABC=∠EDF-∠ADC,
即∠ABE=∠CDF.
点评 本题考查了平行四边形的判断和性质,得到四边形EBFD是平行四边形,是证题的关键.

练习册系列答案
相关题目
2. 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )
 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )| A. | 130° | B. | 110° | C. | 100° | D. | 70° |
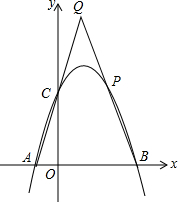 抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标.
抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标.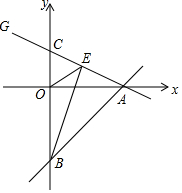 如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE.
如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE. 已知,如图,AB∥CD,∠1=∠2,那么∠E和∠F相等吗?为什么?
已知,如图,AB∥CD,∠1=∠2,那么∠E和∠F相等吗?为什么?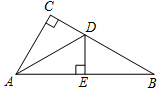 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.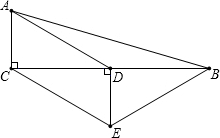 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.