题目内容
18.二次函数y=ax2-bx+b(a>0,b>0)图象的顶点的纵坐标不大于$-\frac{b}{2}$,且图象与x轴交于A,B两点,则线段AB长度的最小值是2$\sqrt{3}$.分析 易求得顶点坐标,即可取得a、b的大小关系,再根据一元二次方程求根公式即可求得AB长度(用a、b表示),即可解题.
解答 解:∵抛物线顶点横坐标为x=-$\frac{-b}{2a}$=$\frac{b}{2a}$,
代入得:y=a${(\frac{b}{2a})}^{2}$-$\frac{{b}^{2}}{2a}$=b≤-$\frac{b}{2}$,
化简得:$\frac{b}{2a}$≥3,即b≥6a,(此时△>0,符合题意)
∵当y=ax2-bx+b=0,时,x1=$\frac{b+\sqrt{{b}^{2}-4ab}}{2a}$,x2=$\frac{b-\sqrt{{b}^{2}-4ab}}{2a}$,
∴AB=$\frac{\sqrt{{b}^{2}-4ab}}{a}$,
∵a、b均大于0,
∴当b=6a时,AB有最小值为2$\sqrt{3}$,
故答案为 2$\sqrt{3}$.
点评 本题考查了一元二次方程的求根公式,考查了二次函数的最小值问题,本题中用a、b表示AB的长度是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.一个正多边形的边长为2,每个外角都为60°,则这个多边形的周长是( )
| A. | 8 | B. | 12 | C. | 16 | D. | 18 |
3. 如图,?ABCD中,下列说法一定正确的是( )
如图,?ABCD中,下列说法一定正确的是( )
 如图,?ABCD中,下列说法一定正确的是( )
如图,?ABCD中,下列说法一定正确的是( )| A. | AB=BD | B. | AC⊥BD | C. | AB=CD | D. | AB=BC |
7. 某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
(1)请你在已建立的平面直角坐标系中,通过①描点、连线,②猜测l与t之间的函数关系,③求出函数的解析式,④验证,这四个步骤确定l与t之间的函数关系;
(2)已知学校的大门宽为5米,问将校门完全关闭再完全打开共用多少秒?
 某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:| t(秒) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| l(米) | 1 | 1.4 | 1.8 | 2.2 | 2.6 | 3.0 | … |
(2)已知学校的大门宽为5米,问将校门完全关闭再完全打开共用多少秒?
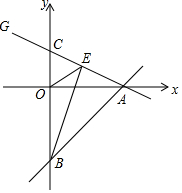 如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE.
如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE.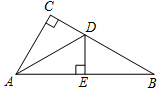 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.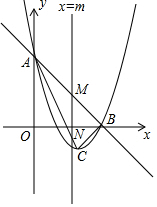 如图,已知抛物线y=x2+bx+c与直线y=-x+3相交于坐标轴上的A,B两点,顶点为C.
如图,已知抛物线y=x2+bx+c与直线y=-x+3相交于坐标轴上的A,B两点,顶点为C.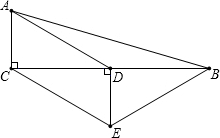 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.