题目内容
11.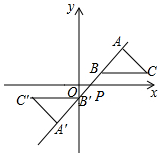 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3).
如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3).
分析 根据等腰直角三角形,可得AB的长,再根据锐角三角函数,可得AD,BD的长,再根据待定系数法,可得函数解析式,根据自变量与函数值得对应关系,可得P点坐标,根据中点坐标公式,可得答案.
解答 解:如图 ,
,
点B,C的坐标为(2,1),(6,1),得
BC=4.
由∠BAC=90°,AB=AC,
得AB=2$\sqrt{2}$,∠ABD=45°,
∴BD=AD=2,
A(4,3),
设AB的解析式为y=kx+b,将A,B点坐标代入,得
$\left\{\begin{array}{l}{2k+b=1}\\{4k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
AB的解析式为y=x-1,
当y=1时,x=1,即P(1,0),
由中点坐标公式,得
xA′=2xP-xA=2-4=-2,
yA′=2yA′-yA=0-3=-3,
A′(-2,-3).
故答案为:(-2,-3).
点评 本题考查了等腰直角三角形,利用等腰直角三角形得出AB的长是解题关键.

练习册系列答案
相关题目
1.在实数-1,0,3,$\frac{1}{2}$中,最大的数是( )
| A. | -1 | B. | 0 | C. | 3 | D. | $\frac{1}{2}$ |
2. 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )
 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )| A. | 130° | B. | 110° | C. | 100° | D. | 70° |
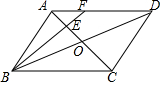 如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
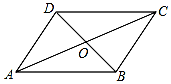 如图,在?ABCD中,对角线AC与BD相交于点O,△AOB的周长与△AOD的周长之和为12cm,两条对角线长之和为7cm,则这个平行四边形的周长为10cm.
如图,在?ABCD中,对角线AC与BD相交于点O,△AOB的周长与△AOD的周长之和为12cm,两条对角线长之和为7cm,则这个平行四边形的周长为10cm.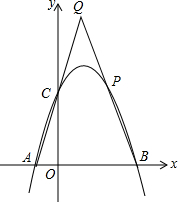 抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标.
抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标.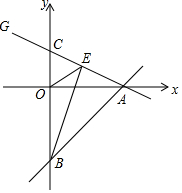 如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE.
如图,直线y=x-4与x轴交于点A,与y轴交于点B,若C(0,2),BE⊥AC于E.连OE.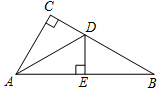 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.