题目内容
7. 数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下
数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AB的中点,那么线段OC的长度是5.5.
学生小明读完题后,稍微一想就画出了如图所示图形,并进行了解答:
因为 AB=5cm
又因为 O是线段AB的中点,
所以OA=OB=$\frac{1}{2}$AB
所以OA=OB=2.5.
因为OC=OB+BC
又因为BC=3cm.
所以OC=5.5.
(1)请你帮助小明将其解答过程补充完整;
(2)学生小惠看完小明的展示后,对其进行了质疑,她认为小明对此题的考虑不全面,忽略了一种情况;请你把小明忽略的那种情况画出图形来,并模仿(1)中的各式进行解答.
分析 (1)当点C在线段AB的延长线上时,AB=5,如果点O是线段AB的中点,则线段OB=$\frac{1}{2}$AB,再根据线段的和差,可得答案.
(2)当点C在线段AB上时,AB=5,如果点O是线段AB的中点,则线段OB=$\frac{1}{2}$AB,再根据线段的和差,可得答案.
解答 解:(1)因为 AB=5cm
又因为 O是线段AB的中点,
所以OA=OB=$\frac{1}{2}$AB
所以OA=OB=2.5.
因为OC=OB+BC
又因为BC=3cm.
所以OC=5.5,
故答案为:$\frac{1}{2}$AB,OB,BC,5.5;
(2)AB=5cm
又因为 O是线段AB的中点,
所以OA=OB=$\frac{1}{2}$AB
所以OA=OB=2.5.
因为OC=BC-OB,
又因为BC=3cm.
OC=3-2.5=0.5cm.
点评 本题考查了两点间的距离,利用线段中点的性质得出OB的长是解题关键,又利用了线段的和差.

练习册系列答案
相关题目
17.已知∠C=75°,则∠A与∠B满足以下哪个选项才能构成△ABC( )
| A. | sinA=$\frac{\sqrt{2}}{2}$,sinB=$\frac{\sqrt{2}}{2}$ | B. | cosA=$\frac{1}{2}$,cosB=$\frac{\sqrt{3}}{2}$ | C. | sinA=$\frac{\sqrt{2}}{2}$,tanB=$\sqrt{3}$ | D. | sinA=$\frac{\sqrt{3}}{2}$,cosB=$\frac{1}{2}$ |
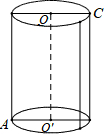 如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)
如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)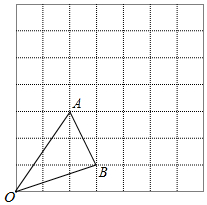 如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:
如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题: