题目内容
15．已知$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b为常数，且ab≠0）表示焦点在x轴上的双曲线，若$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m-4}$=1表示焦点在x轴上的双曲线，则m的取值范围是（ ）| A． | m＞2 | B． | m＞-3 | C． | m≥-3 | D． | -3＜m＜2 |
分析 根据解不等式组的方法解答即可．
解答 解：∵$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m-4}$=1表示焦点在x轴上的双曲线，
∴$\left\{\begin{array}{l}{m+3＞0}\\{2m-4＜0}\end{array}\right.$，
解得：-3＜m＜2，
故选D．
点评 本题考查了不等式组的解集，正确的解答不等式组是解题的关键．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6．
一个不等式组中两个不等式的解集如图所示，则这个不等式组的解集为（ ）
一个不等式组中两个不等式的解集如图所示，则这个不等式组的解集为（ ）| A． | 0≤x≤$\frac{1}{3}$ | B． | x≤$\frac{1}{3}$ | C． | 0≤x＜$\frac{1}{3}$ | D． | x＞0 |
20．以下列各组数为边长首尾相连，能构成直角三角形的一组是（ ）
| A． | 2，3，4 | B． | 1，2，$\sqrt{3}$ | C． | 5，12，17 | D． | 6，8，12 |
数学课上，王老师在黑板上出示了一道问题让大家回答：题目如下
5．
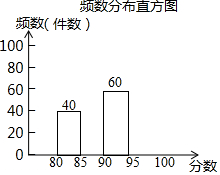某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动，全县有1000名学生的作品（每人1件作品）参加了这个评比活动，评比的方法是给每件作品一个分值，最高分100分，最低分80分．现从这1000件作品中随机抽取了m件作品，并把这m件作品的分值制成了如下频数分布表和频数分布直方图：
（1）求出m的值；
（2）补全频数分布表和频数分布直方图；
（3）如果作品的分值在95分（含95分）以上的可以获得一等奖，试估计全县参加此项活动获得一等奖的人数．
某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动，全县有1000名学生的作品（每人1件作品）参加了这个评比活动，评比的方法是给每件作品一个分值，最高分100分，最低分80分．现从这1000件作品中随机抽取了m件作品，并把这m件作品的分值制成了如下频数分布表和频数分布直方图：| 分数段 | 频数 | 百分比 |
| 80≤x＜85 | 40 | 20% |
| 85≤x＜90 | 80 | 40% |
| 90≤x＜95 | 60 | 30% |
| 95≤x＜100 | 20 | 10% |
（2）补全频数分布表和频数分布直方图；
（3）如果作品的分值在95分（含95分）以上的可以获得一等奖，试估计全县参加此项活动获得一等奖的人数．