题目内容
16.甲同学上午8点20分步行去郊游,10点20分乙同学在同一地骑自行车按原路追甲同学.已知甲同学行走的速度为每小时4千米,乙同学要在不超过11点追上甲同学,问乙同学的骑车速度至少要多少?分析 设乙同学的骑车速度为x千米/时,由:甲同学行的路程≤乙同学行的路程,解出x值.
解答 解:设乙同学的骑车速度为x千米/时,
11点-8点20分=$\frac{8}{3}$小时
依题意得:4×$\frac{8}{3}$≤$\frac{2}{3}$x,
解得x≥16.
所以x最小值为16.
答:乙同学要在不超过11点追上甲同学,乙同学的骑车速度至少要16千米/时.
点评 本题考查了一元一次不等式的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的数量关系.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
6. 一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集为( )
一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集为( )
 一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集为( )
一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集为( )| A. | 0≤x≤$\frac{1}{3}$ | B. | x≤$\frac{1}{3}$ | C. | 0≤x<$\frac{1}{3}$ | D. | x>0 |
5.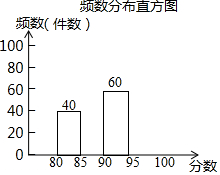 某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
(1)求出m的值;
(2)补全频数分布表和频数分布直方图;
(3)如果作品的分值在95分(含95分)以上的可以获得一等奖,试估计全县参加此项活动获得一等奖的人数.
 某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:| 分数段 | 频数 | 百分比 |
| 80≤x<85 | 40 | 20% |
| 85≤x<90 | 80 | 40% |
| 90≤x<95 | 60 | 30% |
| 95≤x<100 | 20 | 10% |
(2)补全频数分布表和频数分布直方图;
(3)如果作品的分值在95分(含95分)以上的可以获得一等奖,试估计全县参加此项活动获得一等奖的人数.
 数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下
数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下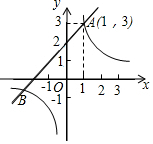 如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).
如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3). 如图,过等腰直角三角板ABC顶点C作AB边的平行线CD,再作∠BCD的平分线CE,则∠BCE=22.5°.
如图,过等腰直角三角板ABC顶点C作AB边的平行线CD,再作∠BCD的平分线CE,则∠BCE=22.5°.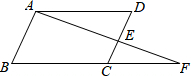 如图,已知:∠DAF=∠F,∠B=∠D,试说明AB∥DC.下面是解答过程,请你在括号内填写理由.
如图,已知:∠DAF=∠F,∠B=∠D,试说明AB∥DC.下面是解答过程,请你在括号内填写理由.