题目内容
19.在平面直角坐标系中,O为坐标原点,设P(3,t)在反比例函数y=$\frac{12}{x}$的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP,若反比例函数y=$\frac{k}{x}$的图象经过点Q,则k=-8或32.分析 把P点代入y=$\frac{12}{x}$求得P的坐标,进而求得OP的长,由QP=OP即可求得Q的坐标,从而求得k的值.
解答 解:∵点P(3,t)在反比例函数y=$\frac{12}{x}$的图象上,
∴t=$\frac{12}{3}$=4,
∴P(3,4),
∴OP=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.
∴Q(-2,4)或(8,4)
∵反比例函数y=$\frac{k}{x}$的图象经过点Q,
∴4=$\frac{k}{-2}$或4=$\frac{k}{8}$,
解得k=-8或32,
故答案为:-8或32.
点评 本题考查了反比例函数图象上点的坐标特征,勾股定理的应用,求得Q点的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下
数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下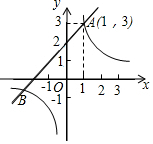 如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).
如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3). 如图,过等腰直角三角板ABC顶点C作AB边的平行线CD,再作∠BCD的平分线CE,则∠BCE=22.5°.
如图,过等腰直角三角板ABC顶点C作AB边的平行线CD,再作∠BCD的平分线CE,则∠BCE=22.5°.