题目内容
2.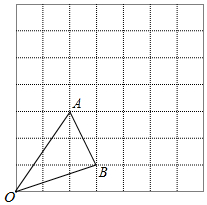 如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:
如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:(1)以O为位似中心,将△OAB放大2倍后作出对应△OA′B′,(其中A、B对应点分别为A′、B′,且A′、B′均在图中格点中)
(2)若线段A′B′上有一点P(m,n),则点P在AB上的对应点P′的坐标为($\frac{m}{2}$,$\frac{n}{2}$).
(3)若△OAB的面积为k,则△OA′B′的面积是4S.
分析 (1)作出对应点A′、B′即可;
(2)利用位似图形的性质即可解决问题;
(3)利用相似三角形的性质即可解决问题;
解答 解:(1)△OA′B′如图所示.
(2)∵线段A′B′上有一点P(m,n),点P在AB上的对应点P′的坐标,
∴P($\frac{m}{2}$,$\frac{n}{2}$).
(3)由题意△OAB∽△OA′B′,
∴$\frac{{S}_{△OAB}}{{S}_{△OA′B′}}$=($\frac{1}{2}$)2,
∵S△OAB=S,
∴S△OA′B′=4S.
故答案为 ($\frac{m}{2}$,$\frac{n}{2}$),4S.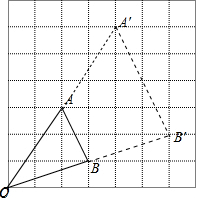
点评 本题考查作图-位似图形、三角形的面积等知识,解题的关键是熟练掌握位似图形的性质,即可解决问题,属于中考常考题型.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,∠AOB
如图,∠AOB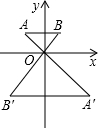 如图,已知△OAB与△OA′B′是相似比为1:2的位似图形,点O是位似中心,若OA=2,则AA′的长是( )
如图,已知△OAB与△OA′B′是相似比为1:2的位似图形,点O是位似中心,若OA=2,则AA′的长是( )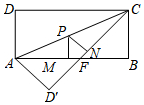 如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.
如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F. 数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下
数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下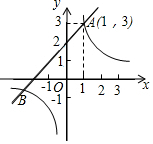 如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).
如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).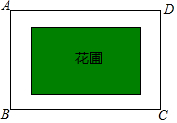 如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,学校计划在一块长为60米,宽为40米的长方形空地ABCD内修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.