题目内容
14.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(-2,1)的对应点为A′(3,-1),点B的对应点为B′(4,0),则点B的坐标为( )| A. | (9,-2) | B. | (-1,-2) | C. | (9,2) | D. | (-1,2) |
分析 直接利用平移中点的变化规律求解即可.
解答 解:横坐标从-2到3,说明是向右移动了3-(-2)=5,纵坐标从1到-1,说明是向下移动了1-(-1)=2,
求原来点的坐标,则为让新坐标的横坐标都减5,纵坐标都加2.
则点B的坐标为(-1,2).
故选D.
点评 本题考查了图形的平移变换,注意左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.求原来点的坐标正好相反.

练习册系列答案
相关题目
4.在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
(1)按表格数据格式,表中的a=123;b=0.404;
(2)请估计:当次数s很大时,摸到白球的频率将会接近0.4(精确到0.1);
(3)请推算:摸到红球的概率是0.6(精确到0.1);
(4)试估算:这一个不透明的口袋中红球有15只.
| 摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
| 摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
| 摸到白球的频率$\frac{n}{s}$ | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(2)请估计:当次数s很大时,摸到白球的频率将会接近0.4(精确到0.1);
(3)请推算:摸到红球的概率是0.6(精确到0.1);
(4)试估算:这一个不透明的口袋中红球有15只.
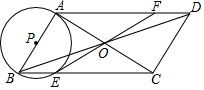 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F.
如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F. 如图,已知点E在正方形ABCD在内,AE=6,BE=8,AB=10,求图中阴影部分的面积S.
如图,已知点E在正方形ABCD在内,AE=6,BE=8,AB=10,求图中阴影部分的面积S. 如图,一次函数y=kx+1的图形经过点A(1,2),且与x轴相交于点B,若点P是y轴上一点,且满足△APB是等腰三角形,则点P的坐标可以是(0,2+$\sqrt{7}$),(0,2-$\sqrt{7}$),(0,$\sqrt{7}$),(0,-$\sqrt{7}$).
如图,一次函数y=kx+1的图形经过点A(1,2),且与x轴相交于点B,若点P是y轴上一点,且满足△APB是等腰三角形,则点P的坐标可以是(0,2+$\sqrt{7}$),(0,2-$\sqrt{7}$),(0,$\sqrt{7}$),(0,-$\sqrt{7}$). 完成下面的证明:
完成下面的证明: