题目内容
4.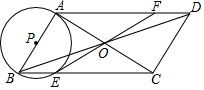 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F.
如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD,∠BAC=90°,以AB为直径的⊙P交BC于点E,连接EO并延长交AD于点F.(1)求证:OE是⊙P的切线;
(2)OA=OF.
分析 (1)连接PE、AE.依据直径所对的圆周角是90°可得到∠AEB=90°,依据同角的余角相等可证明∠ABE=∠EAO,然后利用直角三角形斜边上中线的性质可得到OA=OE,从而可证明∠OAE=∠OEA,于是可得到∠ABE=∠AEO,接下来再证明∠PEA+∠AEO=90°即可;
(2)先证明OA是⊙P的切线,依据切线长定理可得到OA=OE,接下来证明四边形ABCD为平行四边形,从而可得到AD∥BC,然后证明△DFO≌△BEO可得到OE=OF,通过等量代换可得到OA=OF.
解答 解:(1)如图所示:连接PE、AE.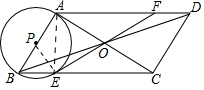
∵AB是⊙O的直径,
∴∠AEB=∠AEC=90°.
∵∠ABE+∠BAE=90°,∠BAE+∠EAC=90°,
∴∠ABE=∠EAO.
∵OA=OC,
∴OA=OE=$\frac{1}{2}$AC.
∴∠OAE=∠OEA.
∴∠ABE=∠AEO.
∵PE=PA,
∴∠PAE=∠PEA.
∴∠PEA+∠AEO=∠ABE+∠BAE=90°.
∴∠OEP=90°,
∴OE是⊙O的切线;
(2)∵点A在⊙P上,∠BAO=90°,
∴OA是⊙P的切线.
又∵OE为⊙P的切线,
∴OA=OE.
∵OA=OC,OB=OD,
∴四边形ABCD为平行四边形.
∴AD∥BC.
∴∠FDO=∠EBO.
在△DFO和△BEO中$\left\{\begin{array}{l}{∠BOE=∠DOF}\\{∠FDO=∠EBO}\\{OB=OD}\end{array}\right.$,
∴△DFO≌△BEO.
∴OE=OF.
∴OA=OF.
点评 本题考查了切线的判定,平行四边形的性质和判定,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
18.在下列说法中:①10的平方根是±$\sqrt{10}$;②-2是4的一个平方根;③$\frac{4}{9}$的平方根是$\frac{2}{3}$;④0.01的算术平方根是0.1;⑤$\sqrt{(-2)^{2}}$=2,正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9. 如图,若“帅”的位置用(1,-1)表示,“馬”的位置用(4,-1)表示,则“兵”的位置可表示为( )
如图,若“帅”的位置用(1,-1)表示,“馬”的位置用(4,-1)表示,则“兵”的位置可表示为( )
 如图,若“帅”的位置用(1,-1)表示,“馬”的位置用(4,-1)表示,则“兵”的位置可表示为( )
如图,若“帅”的位置用(1,-1)表示,“馬”的位置用(4,-1)表示,则“兵”的位置可表示为( )| A. | (-1,2) | B. | (-1,-2) | C. | (-3,-2) | D. | (-3,2) |
14.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(-2,1)的对应点为A′(3,-1),点B的对应点为B′(4,0),则点B的坐标为( )
| A. | (9,-2) | B. | (-1,-2) | C. | (9,2) | D. | (-1,2) |
 如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,AD=BD.
如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,AD=BD.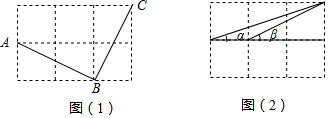
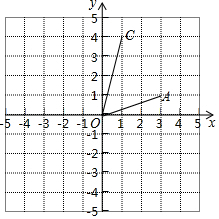 如图,在直角坐标系中,已知点B的位置满足OA∥BC,OC∥AB.
如图,在直角坐标系中,已知点B的位置满足OA∥BC,OC∥AB.