题目内容
3. 完成下面的证明:
完成下面的证明:如图,已知∠BAG与∠AGD互补,且∠1=∠2,求证:∠E=∠F.
证明:∵∠BAG与∠AGD互补(已知).
∴AB∥CD(同旁内角互补两直线平行)
∴∠BAG=∠AGC(两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠BAG-∠1=∠AGC-∠2(等式的性质)
即∠3=∠4
∴AE∥FG(内错角相等,两直线平行)
∴∠E=∠F(两直线平行,内错角相等)
分析 已知∠BAP与∠AGD互补,根据同旁内角互补两直线平行,可得AB∥CD,再根据平行线的判定与性质及等式相等的性质即可得出答案.
解答 证明:∵∠BAG与∠AGD互补(已知),
∴AB∥CD (同旁内角互补两直线平行),
∴∠BAG=∠AGC (两直线平行,内错角相等),
又∵∠1=∠2(已知)
∴∠BAG-∠1=∠AGC-∠2(等式的性质)
即∠3=∠4
∴AE∥FG (内错角相等,两直线平行).
∴∠E=∠F (两直线平行,内错角相等).
故答案为:AB,CD 同旁内角互补两直线平行,AGC,两直线平行,内错角相等,FG,内错角相等,两直线平行,两直线平行,内错角相等.
点评 本题考查了平行线的判定与性质,属于基础题,关键是正确理解与运用平行线的判定与性质.

练习册系列答案
相关题目
14.在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(-2,1)的对应点为A′(3,-1),点B的对应点为B′(4,0),则点B的坐标为( )
| A. | (9,-2) | B. | (-1,-2) | C. | (9,2) | D. | (-1,2) |
18.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{0.1}$ | B. | $\sqrt{\frac{1}{2017}}$ | C. | $\sqrt{48}$ | D. | $\sqrt{{a}^{2}+{b}^{2}}$ |
15.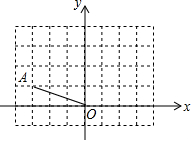 如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )
如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )
 如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )
如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )| A. | (-3,1) | B. | (1,-3) | C. | (1,3) | D. | (3,-1) |
12.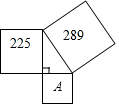 如图,以直角三角形的三边为边向外作正方形,他们的面积依次为225,289,A,则A的值为( )
如图,以直角三角形的三边为边向外作正方形,他们的面积依次为225,289,A,则A的值为( )
 如图,以直角三角形的三边为边向外作正方形,他们的面积依次为225,289,A,则A的值为( )
如图,以直角三角形的三边为边向外作正方形,他们的面积依次为225,289,A,则A的值为( )| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
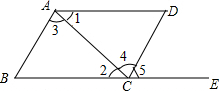 如图,下列能判断AB∥CD的条件有( )个
如图,下列能判断AB∥CD的条件有( )个