题目内容
8.计算:$\frac{1}{a(a+1)}$+$\frac{1}{(a+1)(a+2)}$+$\frac{1}{(a+2)(a+3)}$+…+$\frac{1}{(a+9)(a+10)}$.分析 将各分式根据$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$拆开后两两抵消得$\frac{1}{a}$-$\frac{1}{a+10}$,通分化为同分母分式相减可得.
解答 解:原式=$\frac{1}{a}$-$\frac{1}{a+1}$+$\frac{1}{a+1}$-$\frac{1}{a+2}$+$\frac{1}{a+2}$-$\frac{1}{a+3}$+…+$\frac{1}{a+9}$-$\frac{1}{a+10}$
=$\frac{1}{a}$-$\frac{1}{a+10}$
=$\frac{a+10}{a(a+10)}$-$\frac{a}{a(a+10)}$
=$\frac{10}{a(a+10)}$.
点评 本题主要考查分式的加减法,熟练掌握$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$是解决本题的关键.

练习册系列答案
相关题目
3.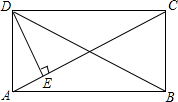 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 22.5° |
3.某校举行文艺汇演,由参加演出的10个班分别派一名代表作为评委,给演出评分,甲、乙两班的评分成绩如表:
(1)若采用平均分进行计算,甲、乙两班哪个班获胜?你认为公平吗?为什么?
(2)采用怎样的方法,对参赛班级更为公平?若采用你提供的方法,甲、乙两班哪个班获胜?
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲班 | 8 | 7 | 7 | 4 | 8 | 7 | 8 | 8 | 8 | 8 |
| 乙班 | 7 | 8 | 8 | 10 | 7 | 7 | 8 | 7 | 7 | 7 |
(2)采用怎样的方法,对参赛班级更为公平?若采用你提供的方法,甲、乙两班哪个班获胜?
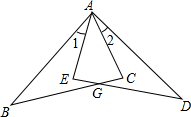 如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG.
如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG. 如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,
如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,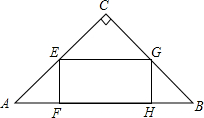 如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.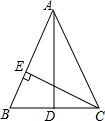 如图,在△ABC中,AB=AC=13,BC=10,D是BC的中点,CE⊥AB于E.
如图,在△ABC中,AB=AC=13,BC=10,D是BC的中点,CE⊥AB于E.