题目内容
20.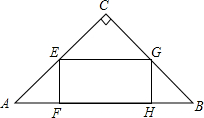 如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
分析 过C作M⊥AB交EG于N,根据矩形的性质得到EG∥FH,由等腰直角三角形的性质得到CM=$\frac{1}{2}$AB=3cm,求得CN=3-EF,根据相似三角形的性质的$\frac{EG}{AB}=\frac{CN}{CM}$,即$\frac{2EF}{6}=\frac{3-EF}{3}$,即可得到结论.
解答 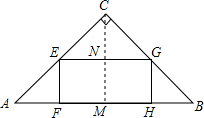 解:过C作M⊥AB交EG于N,
解:过C作M⊥AB交EG于N,
∵四边形EFGH为矩形,
∴EG∥FH,
∴CN⊥EG,
∵△ABC是等腰直角三角形,
∴CM=$\frac{1}{2}$AB=3cm,
∴CN=3-EF,
∵EG∥AB,
∴△CEG∽△ACB,
∴$\frac{EG}{AB}=\frac{CN}{CM}$,即$\frac{2EF}{6}=\frac{3-EF}{3}$,
∴EF=$\frac{3}{2}$,
∴EG=3,
∴矩形EFGH的周长=2($\frac{3}{2}$+3)=9.
点评 此题主要考查了相似三角形的判定与性质,根据矩形性质得出△CEG∽△ACB是解决问题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
10. 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )| A. | 1 | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
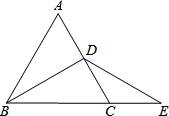 如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.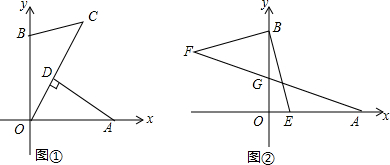
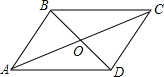 如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.
如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.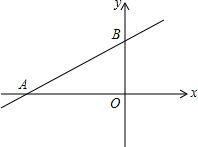 一次函数y=$\frac{\sqrt{3}}{3}$x+3的图象分别交x、y轴于A、B两点,是否在坐标轴上存在一点C使得△ABC为直角三角形?若有,请求出C点的坐标.
一次函数y=$\frac{\sqrt{3}}{3}$x+3的图象分别交x、y轴于A、B两点,是否在坐标轴上存在一点C使得△ABC为直角三角形?若有,请求出C点的坐标.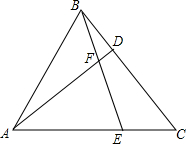 如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.
如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.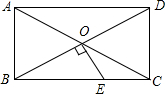 如图,?ABCD的对角线AC、BD交于点O,△AOB是等边三角形.
如图,?ABCD的对角线AC、BD交于点O,△AOB是等边三角形.