题目内容
3.某校举行文艺汇演,由参加演出的10个班分别派一名代表作为评委,给演出评分,甲、乙两班的评分成绩如表:| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲班 | 8 | 7 | 7 | 4 | 8 | 7 | 8 | 8 | 8 | 8 |
| 乙班 | 7 | 8 | 8 | 10 | 7 | 7 | 8 | 7 | 7 | 7 |
(2)采用怎样的方法,对参赛班级更为公平?若采用你提供的方法,甲、乙两班哪个班获胜?
分析 (1)直接利用平均数求法得出两个班级的平均分即可;
(2)去掉一个最高分,再去掉一个最低分,再求平均数,进而得出答案.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{10}$(8+7+7+4+8+7+8+8+8+8)=7.3(分),
$\overline{{x}_{乙}}$=$\frac{1}{10}$(7+8+8+10+7+7+8+7+7+7)=7.6(分)
这样乙获胜,这种方法不公平,因为平均数受极端值的影响;
(2)应该去掉一个最高分,再去掉一个最低分,再求平均数,对参赛班级更为公平,
$\overline{{x}_{甲}}$=$\frac{1}{8}$(8+7+7+8+7+8+8+8)=7.625(分),
$\overline{{x}_{乙}}$=$\frac{1}{8}$(7+8+8+7+7+8+7+7)=7.375(分),
这样甲获胜.
点评 此题主要考查了游戏公平性以及平均数求法,正确理解平均数的意义是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
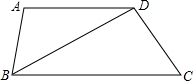 如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.
如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.
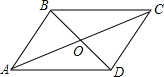 如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.
如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.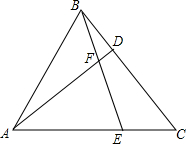 如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.
如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.