题目内容
3.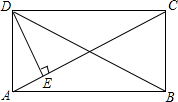 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 22.5° |
分析 根据矩形的性质得出∠ADC=90°,OA=OD,得出∠ADB=∠DAC,由已知条件得出∠ADE=∠ACD=22.5°°,∠CDE=67.5°,求出∠ADB=∠DAC=67.5°,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠ADC=90°,OA=OD,
∴∠ADB=∠DAC,
∵DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,
∴∠ADE=∠ACD=22.5°°,∠CDE=67.5°,
∴∠ADB=∠DAC=67.5°,
∴∠BDC=90°-67.5°=22.5°,
故选:D.
点评 本题考查了矩形的性质、等腰三角形的性质;熟练掌握矩形的性质,弄清各角之间的数量关系是解决问题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
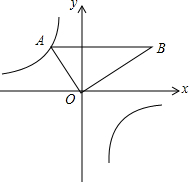 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.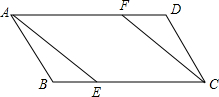 如图,在?ABCD中,已知点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.
如图,在?ABCD中,已知点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.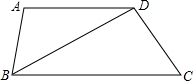 如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.
如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.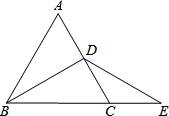 如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.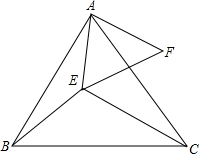 如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.
如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.