题目内容
1.已知abc=1,求$\frac{a}{1+a+ab}$+$\frac{b}{1+b+bc}$+$\frac{c}{1+c+ca}$的值.分析 根据abc=1,把每个分式进行通分,然后进行分式的加法运算即可.
解答 解:原式=$\frac{a}{abc+a+ab}$+$\frac{b}{abc+b+bc}$+$\frac{c}{1+c+ac}$
=$\frac{1}{bc+1+b}$+$\frac{1}{ac+1+c}$+$\frac{c}{1+c+ac}$
=$\frac{ac}{abc•c+ac+abc}$+$\frac{1}{ac+1+c}$+$\frac{c}{1+c+ac}$
=$\frac{ac}{c+ac+1}$++$\frac{1}{ac+1+c}$+$\frac{c}{1+c+ac}$
=$\frac{ac+1+c}{ac+1+c}$
=1.
点评 本题考查了分式的化简求值,把分式进行通分是解决本题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
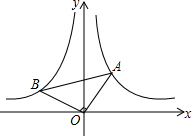 如图,点A是函数$y=\frac{a}{x}(a>0)$的图象在第一象限内分支上一点,过O点作OB⊥OA,交函数$y=-\frac{a}{x}(a>0)$的图象在第二象限内分支于点B.点C为x轴正半轴上一点.
如图,点A是函数$y=\frac{a}{x}(a>0)$的图象在第一象限内分支上一点,过O点作OB⊥OA,交函数$y=-\frac{a}{x}(a>0)$的图象在第二象限内分支于点B.点C为x轴正半轴上一点.