题目内容
10.已知实数a,b满足$\sqrt{3\sqrt{10}-a}$+(b-30$\sqrt{6}$)2=0.(1)求出a,b的值;
(2)若以a的值为长方形的长,b的值为长方形的面积,现要在这个长方形中分割出一个面积最大的正方形,你能求出这个正方形的面积吗?
分析 (1)根据非负数的性质列方程求解即可;
(2)根据长方形的面积求出另一边的长,再确定出正方形的边长,然后根据正方形的面积公式列式计算即可得解.
解答 解:(1)由题意得,3$\sqrt{10}$-a=0,b-30$\sqrt{6}$=0,
解得a=3$\sqrt{10}$,b=30$\sqrt{6}$;
(2)长方形的另一边长=30$\sqrt{6}$÷3$\sqrt{10}$=2$\sqrt{15}$,
∵3$\sqrt{10}$>2$\sqrt{15}$,
∴分割成的正方形的边长为2$\sqrt{15}$,
∴这个正方形的面积=(2$\sqrt{15}$)2=60.
点评 本题考查了二次根式的应用,非负数的性质,长方形的性质,熟练掌握二次根式的运算是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
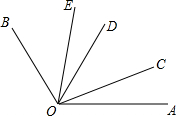 如图,OC,OD,OE是∠AOB内部的三条射线,下面关于∠EOC的表述:①∠EOC=∠BOC-∠BOE;②∠EOC=∠EOD+∠COD;③∠EOC=∠BOC+∠AOE-∠AOB;④∠EOC=∠AOB-∠BOD,其中表述正确的个数有( )
如图,OC,OD,OE是∠AOB内部的三条射线,下面关于∠EOC的表述:①∠EOC=∠BOC-∠BOE;②∠EOC=∠EOD+∠COD;③∠EOC=∠BOC+∠AOE-∠AOB;④∠EOC=∠AOB-∠BOD,其中表述正确的个数有( )