题目内容
6.在△ABC中,∠C=90°,已知∠B=45°,BC=2,求AB,AC,∠A的值.分析 首先在等腰直角三角形ABC中求得AC的长,然后根据勾股定理列式计算即可.
解答 解:∵∠C=90°,∠B=45°,
∴∠A=∠B=45°,
∴AC=BC=2,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
点评 本题考查了解直角三角形,用到的知识点是等腰直角三角形的性质及勾股定理的应用,解题的关键是利用等腰直角三角形的性质求得AC的长.

练习册系列答案
相关题目
16.正多边形的一个外角等于30°,则这个多边形的内角和为( )
| A. | 1080 | B. | 1440 | C. | 1620 | D. | 1800 |
2.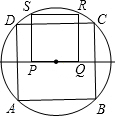 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )| A. | 1:2 | B. | 1:3 | C. | $\sqrt{2}$:3 | D. | 2:5 |