题目内容
7.求证:一条直线截两条平行线所得内错角的角平分线互相平行.分析 根据角平分线的定义得∠1=$\frac{1}{2}$∠BMH,∠2=$\frac{1}{2}$∠CHM,再由两直线平行,内错角相等得∠BMH=∠CHM,则∠1=∠2,然后根据平行线的判定方法即可.
解答 已知AB∥CD,MN平分∠BMH,GH平分∠CHM,
求证:MN∥GH.
证明:∵MN平分∠BMH,GH平分∠CHM,
∴∠1=$\frac{1}{2}$∠BMH,∠2=$\frac{1}{2}$∠CHM,
∵AB∥CD,
∴∠BMH=∠CHM,
∴∠1=∠2,
∴MN∥GH.
点评 本题考查了平行线的判定与性质:同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,两直线平行;两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
19.把抛物线y=-4x2先向上平移2个单位,再向左平移3个单位,所得的抛物线为( )
| A. | y=-4(x+3)2-2 | B. | y=-4(x+3)2+2 | C. | y=-4(x-3)2-2 | D. | y=-4(x-3)2+2 |
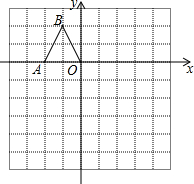 如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.