Question

17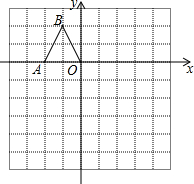．如图，在边长均为1的小正方形网格纸中，△OAB的顶点O、A、B均在格点上，且O是直角坐标系的原点，点A在x轴上．
（1）以O为位似中心，将△OAB放大，使得放大后的△OA₁B₁与△OAB对应线段的比为2：1，画出△OA₁B₁ （所画△OA₁B₁与△OAB在位似中心两侧）．
（2）直接写出线段A₁B₁的长为2$\sqrt{5}$；
（3）在（1）的条件下，若△OAB内一点P（x，y）与△OA₁B₁内一点P′是一对对应点，则点P′的坐标是（-2x，-2y）．

Answer 1

分析 （1）由以O为位似中心，将△OAB放大，使得放大后的△OA₁B₁与△OAB对应线段的比为2：1，画出△OA₁B₁，且所画△OA₁B₁与△OAB在位似中心两侧，根据位似图形的性质，可求得A₁的坐标为：（4，0），B₁的坐标为：（2，-4），继而画出△OA₁B₁；
（2）直接利用勾股定理求解即可求得线段A₁B₁的长；
（3）由位似图形的性质，即可求得点P′的坐标．

解答 解：（1）如图：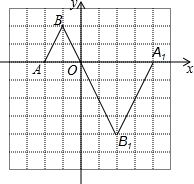


（2）∵A₁的坐标为：（4，0），B₁的坐标为：（2，-4），
∴线段A₁B₁的长为：$\sqrt{（4-2）^{2}+（0-4）^{2}}$=2$\sqrt{5}$；
故答案为：2$\sqrt{5}$；

（3）∵△OAB内一点P（x，y）与△OA₁B₁内一点P′是一对对应点，
∴点P′的坐标是 （-2x，-2y）．

点评 此题考查了位似图形的性质．注意根据题意求得A₁的坐标为：（4，0），B₁的坐标为：（2，-4）是关键．