题目内容
(1)如图1,已知线段AB=6,延长线段AB到C,使BC=2AB,点D是AC的中点.求BD的长;
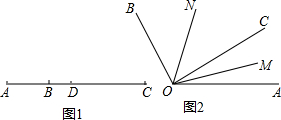
(2)如图2,OC是∠AOB内任一条射线,OM、ON分别平分∠AOC、∠BOC,若∠AOB=100°,请求出∠MON的大小.

(2)如图2,OC是∠AOB内任一条射线,OM、ON分别平分∠AOC、∠BOC,若∠AOB=100°,请求出∠MON的大小.
考点:两点间的距离,角平分线的定义
专题:
分析:(1)由已知条件可知,BC=2AB,AB=6,则BC=12,故AC=AB+BC可求;又因为点D是AC的中点,则AD=
AC,故BD=BC-DC可求.
(2)根据角平分线的性质,可得∠MOC与∠NOC的关系,∠AOM与∠COM的关系,根据角的和差,可得答案.
| 1 |
| 2 |
(2)根据角平分线的性质,可得∠MOC与∠NOC的关系,∠AOM与∠COM的关系,根据角的和差,可得答案.
解答:解:(1)∵BC=2AB,AB=6,
∴BC=12,
∴AC=AB+BC=18,
∵D是AC的中点,
∴AD=
AC=9,
∴BD=BC-DC=12-9=3.
(2)OM、ON分别平分∠AOC、∠BOC,
∴∠NOC=
∠BOC,∠COM=
∠AOC,
∵∠MON=∠MOC+∠COM,∠AOB=100°,
∴∠MON=
(∠BOC+∠AOC)=
∠AOB=50°.
∴BC=12,
∴AC=AB+BC=18,
∵D是AC的中点,
∴AD=
| 1 |
| 2 |
∴BD=BC-DC=12-9=3.
(2)OM、ON分别平分∠AOC、∠BOC,
∴∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠MON=∠MOC+∠COM,∠AOB=100°,
∴∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了两点间的距离,利用了线段中点的性质,线段的和差,角平分线的性质,角的和差.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
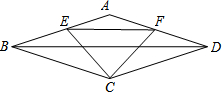 如图,菱形ABCD中,点E,F分别是边AB,AD的中点,连接CE,CF,EF,若四边形ABCD的面积是40cm2,则△CEF的面积为( )
如图,菱形ABCD中,点E,F分别是边AB,AD的中点,连接CE,CF,EF,若四边形ABCD的面积是40cm2,则△CEF的面积为( )| A、5cm2 |
| B、10cm2 |
| C、15cm2 |
| D、20cm2 |
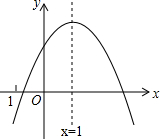 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )| A、①② | B、②③ |
| C、②③④ | D、①②③④ |
若A、O、B三点在同一条直线上,OA=3,OB=5,则A、B两点间的距离为( )
| A、2 | B、8 | C、3 | D、8或2 |
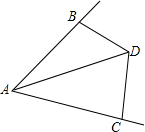 如图,已知AB=AC,∠BAC=60°,∠BDC=120°,求证:AD=BD+CD.
如图,已知AB=AC,∠BAC=60°,∠BDC=120°,求证:AD=BD+CD.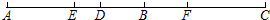 如图,点B、D在线段AC上,BD=
如图,点B、D在线段AC上,BD=