题目内容
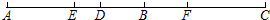 如图,点B、D在线段AC上,BD=
如图,点B、D在线段AC上,BD=| 1 |
| 3 |
| 1 |
| 4 |
考点:两点间的距离
专题:
分析:根据BD、AB、CD的关系,可用BD表示AB,表示CD,根据线段的和差,可得AD,AC的长,根据线段中点的性质,可得AE、FC的长,再根据线段的和差,可得关于BD的方程,根据解方程,可得答案.
解答:解:由BD=
AB=
CD,得
AB=3BD,CD=4BD.
由线段的和差,得
AD=AB-BD=2BD,AC=AD+CD=2BD+4BD=6BD.
由线段AB、CD的中点E、F,得
AE=
AB=
BD,FC=
CD=
BD=2BD.
由线段的和差,得EF=AC-AE-FC=6BD-
BD-2BD=10
解得 BD=4cm,
AB=3BD=3×4=12cm.
| 1 |
| 3 |
| 1 |
| 4 |
AB=3BD,CD=4BD.
由线段的和差,得
AD=AB-BD=2BD,AC=AD+CD=2BD+4BD=6BD.
由线段AB、CD的中点E、F,得
AE=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 4 |
| 2 |
由线段的和差,得EF=AC-AE-FC=6BD-
| 3 |
| 2 |
解得 BD=4cm,
AB=3BD=3×4=12cm.
点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
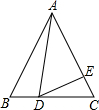 如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为( )
如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为( )| A、4 | B、5 | C、6 | D、7 |
已知∠AOB=60°,OC为∠AOB内部的一条射线,OM、ON分别平分∠AOC和∠BOC,则∠MON等于( )
| A、30° | B、90° |
| C、50° | D、40° |
 如图,线段AD:DE:EF=3:5:3,EF=3cm,求线段AE、AF的长.
如图,线段AD:DE:EF=3:5:3,EF=3cm,求线段AE、AF的长. 已知线段AB,延长AB到C,使BC=
已知线段AB,延长AB到C,使BC=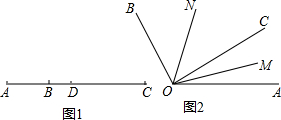
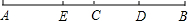 补全下列解题过程.
补全下列解题过程. 如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为
如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为