题目内容
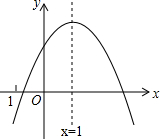 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )| A、①② | B、②③ |
| C、②③④ | D、①②③④ |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线开口方向得到a<0,由抛物线与y轴交点位置得到c>0,则可对①进行判断;利用抛物线的对称方程可对②进行判断;由抛物线与x轴的交点个数可对③进行判断;由于x=-1时函数值小于0,则可对④进行判断.
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线与y轴交点位于y轴正半轴,
∴c>0,
∴ac<0,所以①错误;
∵抛物线的对称轴为直线x=-
=1,
∴b=-2a,即2a+b=0,所以②正确;
∵抛物线与x轴有两个不同的交点,
∴b2-4ac>0,所以③正确;
∵x=-1时,y<0,
∴a-b+c<0,所以④错误.
故选B.
∴a<0,
∵抛物线与y轴交点位于y轴正半轴,
∴c>0,
∴ac<0,所以①错误;
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=-2a,即2a+b=0,所以②正确;
∵抛物线与x轴有两个不同的交点,
∴b2-4ac>0,所以③正确;
∵x=-1时,y<0,
∴a-b+c<0,所以④错误.
故选B.
点评:本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米,将2500000用科学记数法表示应为( )
| A、25×105 |
| B、2.5×106 |
| C、0.25×107 |
| D、2.5×107 |
关于二次函数y=-
(x-5)2+3的图象与性质,下列说法错误的是( )
| 1 |
| 3 |
| A、抛物线开口方向向下 | ||
| B、当x=5时,函数有最大值 | ||
| C、当x>5时,y随x的增大而减小 | ||
D、抛物线可由y=
|
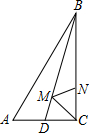 如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是
如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是 已知线段AB,延长AB到C,使BC=
已知线段AB,延长AB到C,使BC=
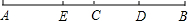 补全下列解题过程.
补全下列解题过程. 如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为
如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为