题目内容
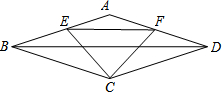 如图,菱形ABCD中,点E,F分别是边AB,AD的中点,连接CE,CF,EF,若四边形ABCD的面积是40cm2,则△CEF的面积为( )
如图,菱形ABCD中,点E,F分别是边AB,AD的中点,连接CE,CF,EF,若四边形ABCD的面积是40cm2,则△CEF的面积为( )| A、5cm2 |
| B、10cm2 |
| C、15cm2 |
| D、20cm2 |
考点:菱形的性质
专题:
分析:如图,作辅助线;证明AC⊥BD,AO=CO(设为λ);证明EF=
BD,AO⊥EF;由△ABD∽△AEF,得到
=
=2,进而得到CM=1.5λ;运用面积公式即可解决问题.
| 1 |
| 2 |
| BD |
| EF |
| AO |
| AM |
解答: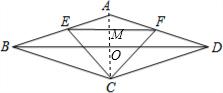 解:如图,连接AC,分别交EF、BD于点M、O;
解:如图,连接AC,分别交EF、BD于点M、O;
∵四边形ABCD为菱形,
∴AC⊥BD,AO=CO(设为λ);
∵点E,F分别是边AB,AD的中点,
∴EF为△ABD的中位线,
∴EF∥BD,EF=
BD,AO⊥EF;
∴△ABD∽△AEF,
∴
=
=2,
∴OM=
OA=0.5λ,CM=1.5λ,
∴
=
=
,
∵SABCD=40,
∴S△EFC=15(cm2).
故选C.
 解:如图,连接AC,分别交EF、BD于点M、O;
解:如图,连接AC,分别交EF、BD于点M、O;∵四边形ABCD为菱形,
∴AC⊥BD,AO=CO(设为λ);
∵点E,F分别是边AB,AD的中点,
∴EF为△ABD的中位线,
∴EF∥BD,EF=
| 1 |
| 2 |
∴△ABD∽△AEF,
∴
| BD |
| EF |
| AO |
| AM |
∴OM=
| 1 |
| 2 |
∴
| S△EFC |
| SABCD |
| ||
|
| ||
| BD•2λ |
∵SABCD=40,
∴S△EFC=15(cm2).
故选C.
点评:该题主要考查了菱形的性质、三角形的中位线定理、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线;灵活运用菱形的性质、三角形的中位线定理、相似三角形的判定等知识点来分析、解答.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,线段AD:DE:EF=3:5:3,EF=3cm,求线段AE、AF的长.
如图,线段AD:DE:EF=3:5:3,EF=3cm,求线段AE、AF的长.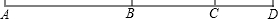 已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.
已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.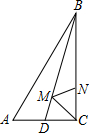 如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是
如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是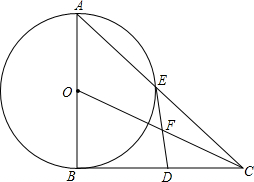 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边上的中点,连接DE.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边上的中点,连接DE. 已知线段AB,延长AB到C,使BC=
已知线段AB,延长AB到C,使BC=