题目内容
若函数y=mx2+2(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为 .
考点:抛物线与x轴的交点,一次函数的性质
专题:分类讨论
分析:当m=0时,函数y=4x+1的图象与x轴有一个交点,当m≠0时,抛物线y=mx2+2(m+2)x+m+1的图象与x轴只有一个交点,即方程mx2+2(m+2)x+m+1=0只有一个根,根据根的判别式为0求出m的值.
解答:解:当m=0时,函数y=4x+1的图象与x轴有一个交点,
当m≠0时,函数y=mx2+2(m+2)x+m+1的图象是抛物线,
若抛物线的图象与x轴只有一个交点,
则方程mx2+2(m+2)x+m+1=0只有一个根,
即4(m+2)2-4m(m+1)=0,
解得m=-
,
综上可得m的值为-
或0,
故答案为-
或0.
当m≠0时,函数y=mx2+2(m+2)x+m+1的图象是抛物线,
若抛物线的图象与x轴只有一个交点,
则方程mx2+2(m+2)x+m+1=0只有一个根,
即4(m+2)2-4m(m+1)=0,
解得m=-
| 4 |
| 3 |
综上可得m的值为-
| 4 |
| 3 |
故答案为-
| 4 |
| 3 |
点评:本题主要考查了抛物线与x轴交点的知识,解答本题的关键是对函数二次项系数m进行分类讨论,此题难度不大,但是很容易出现错误.

练习册系列答案
相关题目
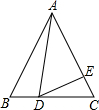 如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为( )
如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为( )| A、4 | B、5 | C、6 | D、7 |
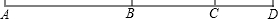 已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.
已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.
 如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为
如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为 如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=45m,EC=15m,CD=10m,则河的宽度AB等于
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=45m,EC=15m,CD=10m,则河的宽度AB等于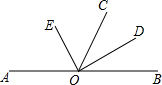 已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.