题目内容
已知二次函数y=ax2+4x+2的图象经过点A(3,-4).
(1)求a的值;
(2)求此函数图象抛物线的顶点坐标;
(3)直接写出函数y随自变量增大而减小的x的取值范围.
(1)求a的值;
(2)求此函数图象抛物线的顶点坐标;
(3)直接写出函数y随自变量增大而减小的x的取值范围.
考点:二次函数的性质
专题:
分析:(1)将点A(3,-4)代入y=ax2+4x+2,即可求出a的值;
(2)利用配方法将一般式化为顶点式,即可求出此函数图象抛物线的顶点坐标;
(3)根据二次函数的增减性即可求解.
(2)利用配方法将一般式化为顶点式,即可求出此函数图象抛物线的顶点坐标;
(3)根据二次函数的增减性即可求解.
解答:解:(1)∵二次函数y=ax2+4x+2的图象经过点A(3,-4),
∴9a+12+2=-4,
∴a=-2;
(2)∵y=-2x2+4x+2=-2(x-1)2+4,
∴顶点坐标为(1,4);
(3)∵y=-2x2+4x+2中,a=-2<0,
抛物线开口向下,对称轴为直线x=1,
∴当x>1时,函数y随自变量增大而减小.
∴9a+12+2=-4,
∴a=-2;
(2)∵y=-2x2+4x+2=-2(x-1)2+4,
∴顶点坐标为(1,4);
(3)∵y=-2x2+4x+2中,a=-2<0,
抛物线开口向下,对称轴为直线x=1,
∴当x>1时,函数y随自变量增大而减小.
点评:本题考查了二次函数的性质.二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
关于二次函数y=-
(x-5)2+3的图象与性质,下列说法错误的是( )
| 1 |
| 3 |
| A、抛物线开口方向向下 | ||
| B、当x=5时,函数有最大值 | ||
| C、当x>5时,y随x的增大而减小 | ||
D、抛物线可由y=
|
二次函数y=-3(x-2)2+4的最大值是( )
| A、2 | B、-2 | C、-3 | D、4 |
已知∠AOB=60°,OC为∠AOB内部的一条射线,OM、ON分别平分∠AOC和∠BOC,则∠MON等于( )
| A、30° | B、90° |
| C、50° | D、40° |
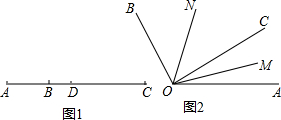
 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=45m,EC=15m,CD=10m,则河的宽度AB等于
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=45m,EC=15m,CD=10m,则河的宽度AB等于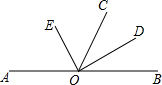 已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.