题目内容
12．已知y=$\sqrt{x-1}$+$\sqrt{5-x}$（x，y均为实数），求当x取何值时，y分别有最大值和最小值．分析 首先根据二次根式有意义的条件确定自变量的取值范围，然后令t=x-3，则-2≤t≤2，得到y=$\sqrt{x-1}$+$\sqrt{5-x}$=$\sqrt{2+t}$+$\sqrt{2-t}$，从而得到-2＜t＜0时，y随着t的增大而增大；当0＜t＜2时y随着t的增加而减小，最后根据其单调性确定最值即可．
解答 解：∵y=$\sqrt{x-1}$+$\sqrt{5-x}$，
∴x-1≥0且5-x≥0，
∴1≤x≤5，
令t=x-3，则-2≤t≤2，
∴y=$\sqrt{x-1}$+$\sqrt{5-x}$=$\sqrt{2+t}$+$\sqrt{2-t}$，
∴当-2＜t＜0时，y随着t的增大而增大；当0＜t＜2时y随着t的增加而减小，
∴t=0，即x=3，y最大值=2$\sqrt{2}$；
t=2和-2，即x=1和5，y最小值=2．
点评 本题考查了无理函数的最值，特别是确定自变量的取值范围是解答本题的关键，将题目中的等式两边平方是解决无理函数的一种重要方法，难度偏大．
练习册系列答案
相关题目
如图，∠AOE是平角，∠COE是直角，∠COD与∠COB互余，∠COD=28°35′，求∠AOB的度数．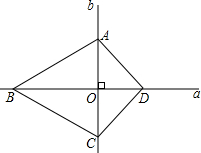
阅读理解应用：我们在课本中学习过，要想比较a和b的大小关系，可以进行作差法，结果如下a-b＞0，a＞b；a-b＜0，a＜b；a-b=0，a=b．
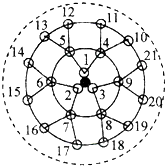生物课题研究小组对附着在物体表面的三个微生物（课题组成员把他们分别标号为1，2，3）的生长情况进行观察记录，这三个微生物第一天各自一分为二产生新的微生物（依次标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录），那么8天所出现的微生物中标号最大的数字是1533号．