Question

7．阅读理解应用：我们在课本中学习过，要想比较a和b的大小关系，可以进行作差法，结果如下a-b＞0，a＞b；a-b＜0，a＜b；a-b=0，a=b．
（1）比较2a²与a²-1的大小，并说明理由．
（2）已知A=2（a²-2a+5），B=3（a²-$\frac{4}{3}$a+4），比较A与B的大小，并说明理由．
（3）比较a²+b²与2ab的大小，并说明理由．
（4）直接利用（3）的结论解决：求a²+$\frac{1}{a^2}$+3的最小值．
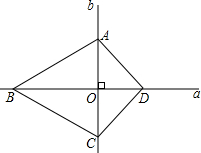
（5）已知如图，直线a⊥b于O，在a，b上各有两点B，D和A，C，且AO=4，BO=9，CO=x²，DO=y²，且xy=3，求四边形ABCD面积的最小值．

Answer 1

分析 （1）（2）（3）直接利用作差法，进一步分解因式，利用非负数的性质判定即可；
（4）利用（3）的结论得出答案即可；
（5）利用四边形ABCD面积等于三角形ABD的面积加上三角形BCD的面积列出式子，利用（3）的结论解决问题．

解答 解：（1）∵2a²-（a²-1）=2a²-a²+1=a²+1＞0，
∴2a²＞a²-1；
（2）A＜B，
理由：∵A-B=2（a²-2a+5）-3（a²-$\frac{4}{3}$a+4）
=2a²-4a+10-3a²+4a-12
=-a²-2＜0，
∴A＜B；
（3）a²+b²≥2ab，
理由：∵a²+b²-2ab=（a^-b）²≥0，
∴a²+b²≥2ab；
（4）a²+$\frac{1}{a^2}$+3≥2a•$\frac{1}{a}$+3=2+3=5
a²+$\frac{1}{a^2}$+3的最小值是5；
（5）∵AO=4，BO=9，CO=x²，DO=y²，且xy=3，
S_{四边形ABCD}=$\frac{1}{2}$×（9+y²）×4+$\frac{1}{2}$×x²（9+y²）
=$\frac{9}{2}$x²+2y²+$\frac{1}{2}$x²y²+18=$\frac{9}{2}$x²+2y²+22.5≥2×$\frac{9}{2}$x•$\frac{2}{3}$y+22.5=18+22.5=40.5，
四边形ABCD面积的最小值是40.5．

点评 此题考查因式分解的实际运用，非负数的性质，作差法是比较两个式子大小常用的方法，掌握完全平方公式是解决问题的关键．