题目内容
6.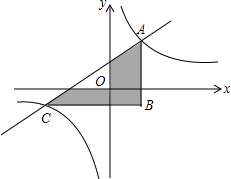 如图,A、C是反比例函数y=$\frac{3}{x}$的图象上的两点,连接AC,过A、C分别作y轴,x轴的平行线,两线交于B,那么阴影部分的面积是6.
如图,A、C是反比例函数y=$\frac{3}{x}$的图象上的两点,连接AC,过A、C分别作y轴,x轴的平行线,两线交于B,那么阴影部分的面积是6.
分析 由A、C是反比例函数y=$\frac{3}{x}$的图象上的两点,设出A(a,$\frac{3}{a}$),则C(-a,-$\frac{3}{a}$),由于AB∥y轴,BC∥x轴,得到B(a,-$\frac{3}{a}$),即可得到S阴影=$\frac{1}{2}$AB•BC=$\frac{1}{2}$•2a•($\frac{3}{a}$$+\frac{3}{a}$)=6.
解答 解:当AC过原点,
∵A、C是反比例函数y=$\frac{3}{x}$的图象上的两点,
设A(a,$\frac{3}{a}$),则C(-a,-$\frac{3}{a}$),
∵AB∥y轴,BC∥x轴,
∴B(a,-$\frac{3}{a}$),
∴S阴影=$\frac{1}{2}$AB•BC=$\frac{1}{2}$•2a•($\frac{3}{a}$$+\frac{3}{a}$)=6.
故答案为:6.
点评 主要考查了反比例函数$y=\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
14.使$\frac{\sqrt{x-3}}{x-4}$有意义的x的取值范围是( )
| A. | x≥3 | B. | x≥3且x≠4 | C. | x≤3 | D. | x<3 |
1.若正多边形的一个外角为60°,则这个正多边形的中心角的度数是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
15.下列各式成立的是( )
| A. | 4<$\sqrt{11}$<5 | B. | (x+1)(x+2)=x2+3x+2 | C. | 2-3=3-2 | D. | x3•x2=x3-x2 |
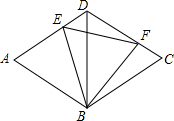 如图,菱形ABCD的较短对角线BD为5$\sqrt{3}$,∠ADB=60°,E、F分别在AD,
如图,菱形ABCD的较短对角线BD为5$\sqrt{3}$,∠ADB=60°,E、F分别在AD,