题目内容
16.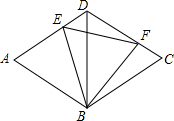 如图,菱形ABCD的较短对角线BD为5$\sqrt{3}$,∠ADB=60°,E、F分别在AD,
如图,菱形ABCD的较短对角线BD为5$\sqrt{3}$,∠ADB=60°,E、F分别在AD,CD上,且∠EBF=60°.
(1)求AE+CF的值;
(2)判断△BEF的形状,并说明理由.
分析 (1)由菱形ABCD中,∠ADB=60°,可证得△ABD与△CBD是等边三角形,继而可得BD=BC,证得△BDE≌△BCF,即可得AE+CF=AE+DE=AD=BD=5$\sqrt{3}$;
(2)由△BDE≌△BCF,可得BE=BF,又由∠EBF=60°,即可证得△BEF是等边三角形.
解答 解:(1)∵四边形ABCD是菱形,
∴AD=AB,
∵∠ADB=60°,
∴△ABD是等边三角形,
同理:△BCD是等边三角形,
∴AD=BD=BC,∠ADB=∠C=60°,
∴∠EBF=∠DBC=60°,
∴∠EBD=∠FBC,
在△DEB和△CFB中,
$\left\{\begin{array}{l}{∠EBD=∠FBC}\\{BD=BC}\\{∠BDE=∠C}\end{array}\right.$,
∴△DEB≌△CFB(ASA),
∴DE=CF,
∴AE+CF=AE+DE=AD=BD=5$\sqrt{3}$;
(2)△BEF是等边三角形,
理由:∵△EDB≌△FCB,
∴BE=BF,
∵∠EBF=60°,
∴△BEF是等边三角形.
点评 此题考查了菱形的性质、全等三角形的判定与性质以及等边三角形的判定与性质.注意证得△ABD与△CBD是等边三角形,继而证得△BDE≌△BCF是关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
1. 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )
 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )| A. | 36° | B. | 54° | C. | 72° | D. | 108° |
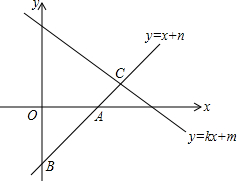 如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论:
如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论: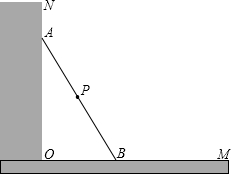 如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.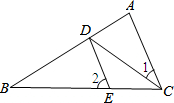 如图,已知CD平分∠ACB,DE∥AC,∠1=40°,则∠2=80°.
如图,已知CD平分∠ACB,DE∥AC,∠1=40°,则∠2=80°.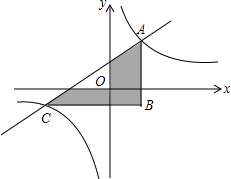 如图,A、C是反比例函数y=$\frac{3}{x}$的图象上的两点,连接AC,过A、C分别作y轴,x轴的平行线,两线交于B,那么阴影部分的面积是6.
如图,A、C是反比例函数y=$\frac{3}{x}$的图象上的两点,连接AC,过A、C分别作y轴,x轴的平行线,两线交于B,那么阴影部分的面积是6.