题目内容
6．一个不透明的袋子中有1个红球，2个黄球，3个白球，除颜色不同外，其他各方面都相同，现从中随机摸出一个球：①这球是“红球”；②这球是“黄球”；③这球是“白球”，将这些事件的序号按发生的可能性从大到小的顺序排列为③②①．分析 根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率，即可求出答案．
解答 解：根据题意可得：袋子中有1个红球，2个黄球，3个白球，共6个，
从袋子中随机摸出一个球，①这球是“红球”的概率是$\frac{1}{6}$；②这球是“黄球”的概率是$\frac{1}{3}$；③这球是“白球”的概率是$\frac{1}{2}$，
故答案为：③②①．
点评 此题考查了概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
名校课堂系列答案
相关题目
17．
如图，正△ABC的边长是2，分别以点B、C为圆心，以r为半径作两条弧，设两弧与边BC围成的阴影部分面积为S，当$\sqrt{2}≤r＜2$时，S的取值范围是（ ）
如图，正△ABC的边长是2，分别以点B、C为圆心，以r为半径作两条弧，设两弧与边BC围成的阴影部分面积为S，当$\sqrt{2}≤r＜2$时，S的取值范围是（ ）| A． | $\frac{π}{2}$-1≤S＜$\frac{4π}{3}$-$\sqrt{3}$ | B． | $\frac{π}{2}$-1≤S＜$\frac{4π}{3}$-1 | C． | 1≤S＜$\sqrt{3}$ | D． | $\sqrt{3}≤S$$＜2\sqrt{3}$-1 |
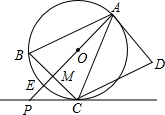如图，AD是⊙O的切线，切点为A，AB是⊙O的弦，过点B作BC∥AD，交⊙O于点C，连接AC，过点C作CD∥AB，交AD于点D，连接AO并延长AO交BC于点M，交$\widehat{BC}$于点E，交过点C的直线于点P，且∠BCP=∠ACD．