题目内容
11.一次函数y=ax+b和二次函数y=ax2+bx在同一平面直角坐标系中的图象可能是( )| A. | 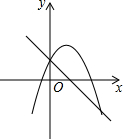 | B. | 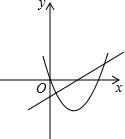 | C. | 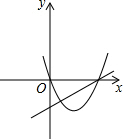 | D. | 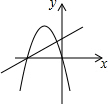 |
分析 根据两个函数的交点坐标可以排除A、B,根据函数的性质可以判断C、D哪个是正确,本题得以解决.
解答 解:$\left\{\begin{array}{l}{y=ax+b}\\{y=a{x}^{2}+bx}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{b}{a}}\\{y=0}\end{array}\right.$
即一次函数y=ax+b和二次函数y=ax2+bx的交点为(0,0)和($-\frac{b}{a},0$),
故A、B错误;
选项C中由一次函数的图象可知,a>0,b<0,则$-\frac{b}{a}>0$,由二次函数图象可知,a>0,b<0,故C正确;
选项D中,由一次函数的图象可知,a>0,b>0,由二次函数的图象可知,a<0,b<0,故选项D错误.
故选C.
点评 本题考查二次函数的性质、一次函数的性质,解题的关键是明确函数的性质,利用数形结合的思想解答问题.

练习册系列答案
相关题目
19.如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B点出发,沿B→C→A运动.如图(1)所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图(2)所示,则图(2)中Q点的坐标是( )
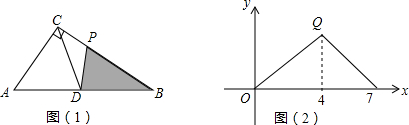

| A. | (4,4) | B. | (4,3) | C. | (4,6) | D. | (4,12) |
13.下列各式是二次根式的是( )
| A. | $\sqrt{-8}$ | B. | $\root{3}{5}$ | C. | $\sqrt{{x}^{2}}$ | D. | $\sqrt{-{x}^{2}-x}$ |
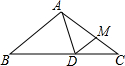 如图,在△ABC中,AB=AC=10,BC=16,D和M分别是BC、AC边上的动点,则AD+DM的最小值是$\frac{48}{5}$.
如图,在△ABC中,AB=AC=10,BC=16,D和M分别是BC、AC边上的动点,则AD+DM的最小值是$\frac{48}{5}$.